题目内容
12. 如图,AB是郑州航空港区某建筑工地的斜坡,其坡度为i=1:2,顶部A处的高AC为8cm,B、C在同一水平地面上.
如图,AB是郑州航空港区某建筑工地的斜坡,其坡度为i=1:2,顶部A处的高AC为8cm,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为某种建筑材料的左视图,其中DE=5m,EF=4m,将建筑材料沿斜坡向上运送,当BF=7m时,求点D离地面的高($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,结果精确到0.1m)
分析 (1)根据坡度定义直接解答即可;
(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据$\frac{GH}{GD}$=$\frac{1}{2}$,得到GH=2m,利用勾股定理求出DH的长,求出BH=10m,进而求出HS,然后得到DS即可.
解答 解:(1)∵坡度为i=1:2,AC=8m,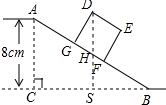
∴BC=2AC=16m.
(2)作DS⊥BC,垂足为S,且与AB相交于H.如图所示:
∵∠DGH=∠BSH,∠DHG=∠BHS,
∴∠GDH=∠SBH,
∴$\frac{GH}{GD}$=$\frac{1}{2}$,
∵DG=EF=4m,
∴GH=2m,
∴DH=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BH=BF+FH=7+(5-2)=10m,
设HS=xm,则BS=2xm,
∴x2+(2x)2=102,
∴x=2$\sqrt{5}$m,
∴DS=2$\sqrt{5}$+2$\sqrt{5}$=4$\sqrt{5}$≈8.9m;
答:点D离地面的高约为8.9m.
点评 本题考查了解直角三角形的应用--坡度坡角问题,熟悉坡度坡角的定义和勾股定理是解题的关键.

练习册系列答案
相关题目
2. 如图,在菱形ABCD中,AB=6,则它的周长是( )
如图,在菱形ABCD中,AB=6,则它的周长是( )
 如图,在菱形ABCD中,AB=6,则它的周长是( )
如图,在菱形ABCD中,AB=6,则它的周长是( )| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
7.已知x=2是方程x2-a2=0的一个根,则a的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 4 |
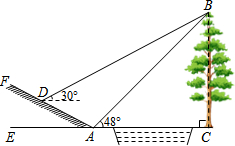 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡脚∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,$\sqrt{3}$≈1.7)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡脚∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.7,cos48°≈0.7,tan48°≈1.1,$\sqrt{3}$≈1.7)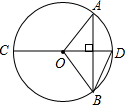 如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD=25°.
如图,CD是⊙O的直径,弦AB⊥CD,若∠AOB=100°,则∠ABD=25°.