题目内容
19. 如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的角平分线,求∠BAD的度数.
如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的角平分线,求∠BAD的度数.
分析 先根据∠BAE=∠CAF=110°,∠CAE=60°,求得∠EAF=50°,以及∠BAF的度数,再根据AD是∠BAF的角平分线,求得∠BAD即可.
解答  解:∵∠BAE=∠CAF=110°,∠CAE=60°,
解:∵∠BAE=∠CAF=110°,∠CAE=60°,
∴∠EAF=∠BAC=110°-60°=50°,
∴∠BAF=110°+50°=160°,
又∵AD是∠BAF的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAF=$\frac{1}{2}$×160°=80°.
点评 本题主要考查了角平分线的定义的运用,解题时注意:若OC是∠AOB的平分线则∠AOC=∠BOC=$\frac{1}{2}$∠AOB或∠AOB=2∠AOC=2∠BOC.解决问题的关键是运用角的和差关系进行计算.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
4.下列抽样方法是随机抽样的是( )
| A. | 为了解刚生产的零件的质量情况,从每一个包装箱内抽5个加以检查 | |
| B. | 为了解全市学生的身高情况,以一、三中的学生为代表进行考察 | |
| C. | 为了解小学生的视力情况,选中六年级20名学生进行调查 | |
| D. | 为了解某地区的车流量,记录某一红绿灯处早上8:00至9:00的车流量 |
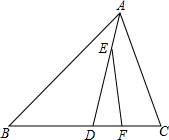 如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°.
如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°. 如图,△ABC中,E为BC的中点,DE⊥BC于E,交AC于D,△ABD的周长为21,AB=10,则AC=11.
如图,△ABC中,E为BC的中点,DE⊥BC于E,交AC于D,△ABD的周长为21,AB=10,则AC=11.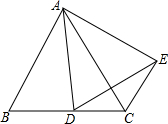 如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数.
如图,△ABC是等边三角形,AD=AE,BD=CE,求∠ACE的度数. 如图,写出平面直角坐标系中各个点的坐标,并指出它们到x轴、y轴的距离分别是多少?
如图,写出平面直角坐标系中各个点的坐标,并指出它们到x轴、y轴的距离分别是多少? 如图所示,求出图中x的值.
如图所示,求出图中x的值.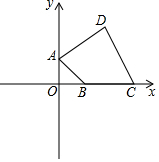 已知:如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(0,1)、B(1,0)、C(3,0)、D(2,2),求四边形ABCD的面积.
已知:如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(0,1)、B(1,0)、C(3,0)、D(2,2),求四边形ABCD的面积.