题目内容
13. 如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,
如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,(1)求边BC的长;
(2)将△ABC绕着点C旋转得△A′B′C,点A的对应点A′,点B的对应点B′.如果点A′在BC边上,那么点B和点B′之间的距离等于多少?
分析 (1)AD⊥BC于点D,由等腰三角形的性质可得BC=2BD,在Rt△ABD中根据AD=ABsinB得出AD,再根据勾股定理即可得BD,从而得出答案;
(2)B′E⊥BC于点E,由旋转的性质得B′C=BC=16,∠ABC=∠ACB=∠A′CB′,在Rt△B′CE中求出B′E、CE的长,由BC=16可得BE的长,继而根据勾股定理可得答案.
解答 解:(1)如图,过点A作AD⊥BC于点D,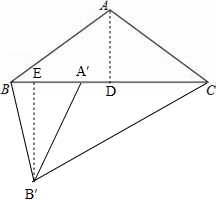
∵AB=AC=10,
∴BC=2BD,
在Rt△ABD中,∵sinB=$\frac{AD}{AB}$,
∴AD=ABsinB=10×$\frac{3}{5}$=6,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=8,
则BC=2BD=16;
(2)过点B′作B′E⊥BC于点E,
根据题意知B′C=BC=16,∠ABC=∠ACB=∠A′CB′,
∴sin∠BCB′=sinB=$\frac{3}{5}$,
∴B′E=B′Csin∠BCB′=16×$\frac{3}{5}$=$\frac{48}{5}$,
∴CE=$\sqrt{B′{C}^{2}-B′{E}^{2}}$=$\frac{64}{5}$,
又∵BC=16,
∴BE=BC-CE=16-$\frac{64}{5}$=$\frac{16}{5}$,
∴BB′=$\sqrt{B{E}^{2}+B′{E}^{2}}$=$\sqrt{(\frac{16}{5})^{2}+(\frac{48}{5})^{2}}$=$\frac{16\sqrt{10}}{5}$.
点评 本题考查了解直角三角形、旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是解Rt△B′CE,利用勾股定理计算BB′的长.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案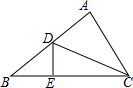 如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )
如图,在△ABC中,∠A=90°,点D是AB边上的一点,过D点作BC的垂线,垂足为点E,已知:AB=4cm,BC=8cm,CD=7cm,则△DBE的周长为( )| A. | 5cm | B. | 6cm | C. | $\frac{9+3\sqrt{3}}{2}$cm | D. | 8cm |
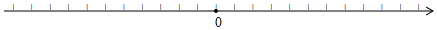
(1)对照数轴填写下表:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.