题目内容
15．
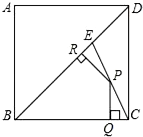如图，E是边长为4的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BR于点R，则PQ+PR的值是$\sqrt{2}$．
分析 连接BP，设点C到BE的距离为h，然后根据S△BCE=S△BCP+S△BEP求出h=PQ+PR，再根据正方形的性质求出h即可．
解答 解：如图，连接BP，设点C到BE的距离为h，
则S△BCE=S△BCP+S△BEP，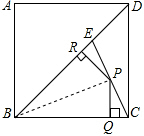
即$\frac{1}{2}$BE•h=$\frac{1}{2}$BC•PQ+$\frac{1}{2}$BE•PR，
∵BE=BC，
∴h=PQ+PR，
∵正方形ABCD的边长为4，
∴h=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．
点评 本题考查了正方形的性质，三角形的面积，熟记性质并作辅助线，利用三角形的面积求出PQ+PR等于点C到BE的距离是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．下列约分中，正确的是（ ）
| A． | $\frac{x^6}{x^2}$=x3 | B． | $\frac{x+y}{x+y}$=0 | C． | $\frac{x+y}{{{x^2}+xy}}=\frac{1}{x}$ | D． | $\frac{{2x{y^2}}}{{4{x^2}y}}=\frac{1}{2}$ |
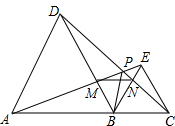如图，A、B、C在一条直线上，△ABD、△BCE均为等边三角形，连接CD、AE交于点P，并分别交BE、BD于N、M，连接MN，下列结论中：①AE=CD；②AM=DP；③MN∥AC； ④若AB=2BC，连接DE，则DE⊥BE；⑤BP平分∠APC．正确的结论有：①③④⑤（填写出所有正确的序号）
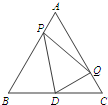如图，△ABC是等边三角形，AB=2，D是边BC的中点．点P从点A出发，沿AB-BD以每秒1个单位长度的速度向终点D运动（点P不与点A、D重合）．同时点Q从点C出发，沿CA-AC以每秒1个单位长度的速度运动．当点P停止运动时，点Q也随之停止运动．设点P的运动时间为t（秒），△PQD的面积为S．