题目内容
5.有一个人患了流感,经过两轮传染后共有121人患了流感;因此一个人传染了10个人,三轮共有1331人患了流感.(期间无人治愈)分析 设第一个人传染了x人,根据两轮传染后共有121人患了流感;列出方程,求解,然后求出三轮之后患流感的人数.
解答 解:设第一个人传染了x人,
由题意得,(x+1)2=121,
解答:x=10,
则第三轮的患病人数为:(10+1)3=1331.
故答案为:10,1331.
点评 本题考查了一元二次方程的应用,解答本题的关键在于读懂题意,设出合适的未知数,找出等量关系,列方程求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
20.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.表是某周的生产情况(超产为正、减产为负):
(1)根据记录可知前三天共生产599辆;
(2)产量最多的一天比产量最少的一天多26辆;
(3)该厂实行每周计件工资制,每生产一辆车可得50元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -4 | +12 | -10 | +16 | -8 |
(2)产量最多的一天比产量最少的一天多26辆;
(3)该厂实行每周计件工资制,每生产一辆车可得50元,那么该厂工人这一周的工资总额是多少?
10.若二次函数y=kx2-kx+1与x轴有两个交点.则k的取值范围是( )
| A. | k>4或k<0 | B. | 0<k<4 | C. | k≥4或k≤0 | D. | 0≤k≤4 |
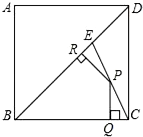 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$.
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$. 如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)
如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)