题目内容
7.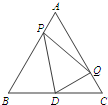 如图,△ABC是等边三角形,AB=2,D是边BC的中点.点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动(点P不与点A、D重合).同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动.设点P的运动时间为t(秒),△PQD的面积为S.
如图,△ABC是等边三角形,AB=2,D是边BC的中点.点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动(点P不与点A、D重合).同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动.设点P的运动时间为t(秒),△PQD的面积为S.(1)求线段CQ的长(用含t的代数式表示).
(2)当△PQD是等边三角形时,求出t的值.
(3)求S与t的函数关系式.
分析 (1)根据当0<t≤2和2<t<3时两种情况进行解答即可;
(2)根据等边三角形的性质和AAS证明△BPD与△CDQ全等解答即可;
(3)根据当0<t≤2和2<t<3时两种情况,利用三角函数和三角形面积公式解答即可.
解答 解:(1)当0<t≤2时,CQ=t.
当2<t<3时,CQ=4-t. 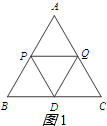
(2)如图1所示;∵△PQD是等边三角形,
∴∠PDQ=60°,
∴∠PDB+∠CDQ=120°,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠PDB+∠BPD=120°,
∴∠BPD=∠CDQ,
∵BD=CD,
在△BPD与△CDQ中,$\left\{\begin{array}{l}{∠BPD=∠CDQ}&{\;}\\{∠B=∠C}&{\;}\\{BD=DC}&{\;}\end{array}\right.$,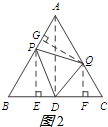
∴△BPD≌△CDQ(AAS),
∴BP=CQ,
∴2-t=t,
∴t=1,
(3)当0<t≤2时,如图2所示,连结AD.
∵△ABC是等边三角形,D是边BC的中点,
∴∠ADB=90°.
∴$AD=AB•sin60°=\sqrt{3}$.
分别过点P、Q作PE⊥BC、QF⊥BC,垂足分别为点E、F.
在Rt△BPE中,∠BEP=90°,$PE=PB•sin60°=\frac{{\sqrt{3}}}{2}(2-t)$.
在Rt△QCF中,∠QFC=90°,$QF=CQ•sin60°=\frac{{\sqrt{3}}}{2}t$.
过点Q作QG⊥AB于点G.在Rt△AGQ中,∠AGQ=90°,$QG=AQ•sin60°=\frac{{\sqrt{3}}}{2}(2-t)$.
∴S△PQD=S△ABC-S△BPD-S△QCD-S△APQ.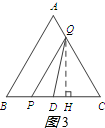
∴${S_{△PQD}}=\frac{1}{2}×2×\sqrt{3}-\frac{1}{2}×\frac{{\sqrt{3}}}{2}(2-t)-\frac{1}{2}×\frac{{\sqrt{3}}}{2}t-\frac{1}{2}×\frac{{\sqrt{3}}}{2}(2-t)t$.
∴$S=\frac{{\sqrt{3}}}{4}{t^2}-\frac{{\sqrt{3}}}{2}t+\frac{{\sqrt{3}}}{2}$.
当2<t<3时,如图3所示,过点Q作QH⊥BC于点H.
在Rt△CQH中,∠CHQ=90°,$QH=CQ•sin60°=\frac{{\sqrt{3}}}{2}(4-t)$.
∴${S_{△PQD}}=\frac{1}{2}PD•QH=\frac{1}{2}×(3-t)\frac{{\sqrt{3}}}{2}(4-t)=\frac{{\sqrt{3}}}{4}{t^2}-\frac{{7\sqrt{3}}}{4}t+3\sqrt{3}$.
∴$S=\frac{{\sqrt{3}}}{4}{t^2}-\frac{{7\sqrt{3}}}{4}t+3\sqrt{3}$.
点评 本题是一道综合性较强的题目,考查了等边三角形的判定和性质、全等三角形的判定与性质、三角函数的性质等知识;是中考压轴题,难度较大.

 阅读快车系列答案
阅读快车系列答案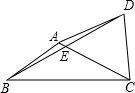 如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.
如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.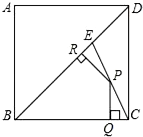 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$.
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$. 如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)
如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)