题目内容
5.某大型超市的采购人员先后购进两批晋祠大米,购进第一批大米共花费5400元,进货单价为m元/千克,该超市将其中3000千克优等品以进货单价的两倍对外出售,余下的二等品则以1.5元/千克的价格出售.当第一批大米全部售出后,花费5000元购进了第二批大米,这一次的进货单价比第一批少了0.2元.其中优等品占总重量的一半,超市以2元/千克的单价出售优等品,余下的二等品在这批进货单价的基础上每千克加价0.6元后全部卖完,若不计其他成本,则售完第二批大米获得的总利润是4000元(总售价-总进价=总利润)(1)用含m的代数式表示第一批大米的总利润.
(2)求第一批大米中优等品的售价.
分析 (1)用总销售额减去成本即可求出毛利润;
(2)设第一批进货单价为m元/千克,则第二批的进货单价为m-2元/千克,根据第二批大米获得的毛利润是4000元,列方程求解.
解答 解:(1)由题意得,总利润为:3000×2m+1.5×($\frac{5400}{m}$-3000)-5400
=6000m+$\frac{8100}{m}$-9900;
(2)设第一批进货单价为m元/千克,
由题意得,$\frac{5000}{m-0.2}$×$\frac{1}{2}$×2+$\frac{5000}{m-0.2}$×$\frac{1}{2}$×(m-0.2+0.6)-5000=4000,
解得:m=1.2,
经检验:m=1.2是原分式方程的解,且符合题意.
则售价为:2m=2.4.
答:第一批大米中优等品的售价是2.4元.
点评 本题考查了方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个计算程序,若输入a的值为-2,则输出的结果应为-2008.
如图是一个计算程序,若输入a的值为-2,则输出的结果应为-2008. 如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.
如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.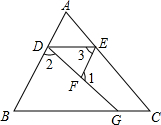 如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.
如图,D、E、F分别是直线AB、AC、DG上的点,已知∠1+∠2=180°,∠3=∠B,∠C=50°,求∠AED的度数.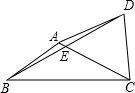 如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.
如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.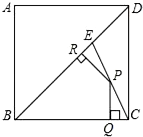 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$.
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是$\sqrt{2}$.