题目内容
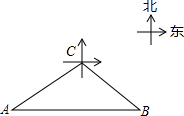 已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,
已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,| 2 |
| 5 |
考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意可以算出:AB之间的距离为40km,BC之间的距离为20km.其次,从C点做AB的垂线(辅助线),并且交AB于D点.根据勾股定理可以得出:AD2+CD2=AC2,BD2+CD2=BC2,求出AD、AC.
解答: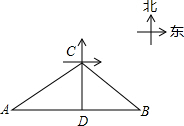 解:∵AB=80×
解:∵AB=80×
=40km,BC=80×
=20km.
根据勾股定理可以得出:
AD2+CD2=AC2,BD2+CD2=BC2,
在以上式子中,设AD为x,那么BD=40-x,
设AC为y,又因为∠ACD=63.4°,
所以CD=x•tan26.6°,
根据以上设定可列出如下方程组:
,
∴
.
以轮船80km/h的速度从C返回A,所需的时间为:26.832×
=0.3354小时.
 解:∵AB=80×
解:∵AB=80×| 1 |
| 2 |
| 1 |
| 4 |
根据勾股定理可以得出:
AD2+CD2=AC2,BD2+CD2=BC2,
在以上式子中,设AD为x,那么BD=40-x,
设AC为y,又因为∠ACD=63.4°,
所以CD=x•tan26.6°,
根据以上设定可列出如下方程组:
|
∴
|
以轮船80km/h的速度从C返回A,所需的时间为:26.832×
| 1 |
| 80 |
点评:考查了解直角三角形的应用-方向角问题,本题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
 如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD=
如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD= 已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值.
已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值. 如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?
如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?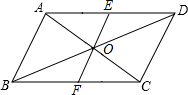 如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:
如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证: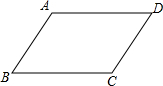 如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线) 如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号)
如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号)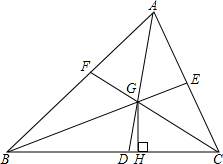 如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.
如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.