题目内容
13.在平面直角坐标系中,点A(x1,y1),B(x2,y2)之间的距离$AB=\sqrt{{{({{x_1}-{x_2}})}^2}+{{({{y_1}-{y_2}})}^2}}$,由此可求得代数式$\sqrt{{x^2}-2x+2}+\sqrt{{x^2}-8x+25}$的最小值为5.分析 根据原式表示的几何意义是点(x,0)到点(1,1)和(4,3)的距离之和,当点(x,0)在以(1,1)和(4,3)为端点的线段上时其距离之和最小,进而求出即可.
解答 解:$\sqrt{{x^2}-2x+2}+\sqrt{{x^2}-8x+25}$=$\sqrt{(x-1)^{2}+{1}^{2}}$+$\sqrt{(x-4)^{2}+{3}^{2}}$,
故原式表示点(x,0)到(1,1)和(4,3)的距离之和.由两点之间线段最短,点(x,0)在以(1,1)和(4,3)为端点的线段上时,原式值最小.利用公式,原式=5.
故答案是:5.
点评 本题考查了两点间的距离公式.掌握代数式$\sqrt{{x^2}-2x+2}+\sqrt{{x^2}-8x+25}$所表示的几何意义是解题的关键.

练习册系列答案
相关题目
1.受中日钓鱼岛事件的影响,在钓鱼岛被“国有化”的9月份,某日本品牌食用油价格开始回落,食用油批发商批发这种品牌的食用油,每桶在9月份前四周每周的平均销售价格变化如下表:
进入10月份后,由于受中日关系趋于缓和等因素的影响,食用油的价格开始回升,该品牌食用油销售价格y2(元/桶)从10月份第1周的54元/桶,上升至第2周的57元/桶,且销售价格y2(元/桶)与周数x(x为整数)的变化情况满足二次函数:y2=-$\frac{1}{4}$x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了3a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上降价a%进行销售,这样顺利的完成了第三周销售1200桶的任务,且获利12000元,请你参考以下数据,估算出a的整数值(0<a<15).
(参考数据:912=8281,922=9464,932=8649,942=8836)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了3a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上降价a%进行销售,这样顺利的完成了第三周销售1200桶的任务,且获利12000元,请你参考以下数据,估算出a的整数值(0<a<15).
(参考数据:912=8281,922=9464,932=8649,942=8836)
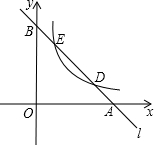 已知直线l分别与x轴、y轴交于A.B两点,与双曲线y=$\frac{a}{x}$(a≠0,x>0)分别交于D.E两点.若点D的坐标为(3,1),点E的坐标为(1,n)
已知直线l分别与x轴、y轴交于A.B两点,与双曲线y=$\frac{a}{x}$(a≠0,x>0)分别交于D.E两点.若点D的坐标为(3,1),点E的坐标为(1,n)