题目内容
18.已知$\frac{{x}_{1}}{{x}_{1}+1}$=$\frac{{x}_{2}}{{x}_{2}+3}$=$\frac{{x}_{3}}{{x}_{3}+5}$=…=$\frac{{x}_{1007}}{{x}_{1007}+2013}$,且x1+x2+…+x1007=10072,则x1007=2013.分析 已知第一个等式利用合比性质化简,将第二个等式代入求出比值,即可确定出x1007的值.
解答 解:∵$\frac{{x}_{1}}{{x}_{1}+1}$=$\frac{{x}_{2}}{{x}_{2}+3}$=$\frac{{x}_{3}}{{x}_{3}+5}$=…=$\frac{{x}_{1007}}{{x}_{1007}+2013}$,且x1+x2+…+x1007=10072,
∴$\frac{{x}_{1}+{x}_{2}+{x}_{3}+…+{x}_{1007}}{{x}_{1}+1+{x}_{2}+3+{x}_{3}+5+…+{x}_{1007}+2013}$=$\frac{{x}_{1007}}{{x}_{1007}+2013}$=$\frac{100{7}^{2}}{100{7}^{2}+(1+3+5+7+…+2013)}$=$\frac{1}{2}$,
∴x1007=$\frac{1}{2}$(x1007+2013),
解得:x1007=2013.
故答案为:2013.
点评 此题考查了解分式方程,熟练掌握比例的性质是解本题的关键.

练习册系列答案
相关题目
8. 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )
 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )| A. |  | B. |  | C. |  | D. |  |
9.下列说法正确的是( )
| A. | 三角形的角平分线、中线、高都在三角形的内部 | |
| B. | 三角形的角平分线、高都在三角形的内部 | |
| C. | 三角形的高、中线都在三角形的内部 | |
| D. | 三角形的角平分线、中线都在三角形的内部 |
10.函数$y=x|x|-2\sqrt{3}x+2$的图象与x轴的交点个数是( )
| A. | 4 | B. | 3 | C. | 1 | D. | 0 |
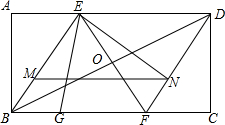 已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.
已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3. 某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: