题目内容
如图，在四边形ABCD中，AB=CD，点MN分别是边AD、BC的中点，O是BD的中点．求证：OM=ON．考点：三角形中位线定理
专题：证明题
分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得OM=
AB，ON=
CD，从而得证．
| 1 |
| 2 |
| 1 |
| 2 |
解答：证明：∵点M、N分别是边AD、BC的中点，O是BD的中点，
∴OM、ON分别是△ABD和△BCD的中位线，
∴OM=
AB，ON=
CD，
∵AB=CD，
∴OM=ON．
∴OM、ON分别是△ABD和△BCD的中位线，
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=CD，
∴OM=ON．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理是解题的关键．
练习册系列答案
相关题目
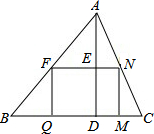有一块锐角三角形铁片ABC，已知最长边BC=12cm，高AD=8cm，要把它加工成一个矩形铁片，使矩形的一边在BC上，其余的两个顶点分别在AB、AC上，且矩形的长是宽的3倍，求矩形的面积．
如图，足球由正五边形和正六边形皮块缝成，试用正六边形的块数x表示正五边形的块数y，并指出其中的变量和常量．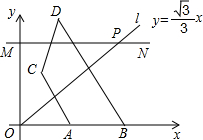
如图，长度为2的动线段AB在x轴上向右移动，设A（x，0），其中x＞0，线段AB关于射线l：y=