题目内容
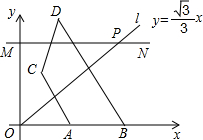 如图,长度为2的动线段AB在x轴上向右移动,设A(x,0),其中x>0,线段AB关于射线l:y=
如图,长度为2的动线段AB在x轴上向右移动,设A(x,0),其中x>0,线段AB关于射线l:y=
| ||
| 3 |
| 3 |
(1)请直接写出结论:
①点P坐标
②当MN平分线段CD时,x=
(2)若线段CD被直线MN分为1:2两部分,求x的值;
(3)设梯形ABDC在直线MN下方部分的面积为y,求y与x的函数关系式,并探究当线段AB在运动过程中y是否存在最大值?若有,请求出最大值;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)①P和M的纵坐标相等,再把纵坐标代入射线l的解析式可求得P点的坐标;②由对称可知O、C、D三点在一条直线上,连接OC,可求得∠POB=∠POD=30°,设CD交MN于点E,在Rt△OME中可求出OE,再用x表示出OE,可解出x的值;
(2)方法同(1)的②;
(3)设DB交MN于点F,可知△OCA、△ODB和△DEF均为等边三角形,则可表示出△OCA、△DEF、△ODB的面积,得出y与x的关系式,再利用函数的性质求最值.
(2)方法同(1)的②;
(3)设DB交MN于点F,可知△OCA、△ODB和△DEF均为等边三角形,则可表示出△OCA、△DEF、△ODB的面积,得出y与x的关系式,再利用函数的性质求最值.
解答: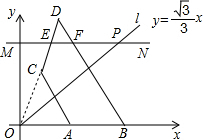
解:
(1)①因为MN平行x轴,所以P点的纵坐标为2
,把y=2
代入解析式y=
x可求得x=6,所以P点坐标为(6,2
),故答案为:(6,2
);
②由对称的性质可知O、C、D三点在一条直线上,连接OC,
因为tan∠POB=
=
,所以∠POB=∠DOP=∠DOM=30°,
设MN交CD于点E,则CE=
CD=
AB=
×2=1,且OC=OA=x,所以OE=x+1,
在Rt△OME中,cos∠EOM=
=
,即
=
,解得x=3,
故答案为:3;
(2)在Rt△OME中,cos∠EOM=
=
,
分两种情况:当CE=2ED时,可知CE=
,则OE=x+
,代入上式可得:
=
,解得x=2
,
当CE=
ED时,可知CE=
,则OE=x+
,代入上式可得:
=
,解得x=3
;
综上可知x的值为2
或3
;
(3)存在,最大值为4
.
设MN交BD于点F,由(1)可知∠COA=60°,且OC=OA,OD=AB,所以△OAC和△OBD都为等边三角形,
又因为MN平行x轴,所以△DEF也为等边三角形,
在RtRt△OME中,可求得OE=4,且OA=x,OB=x+2,所以DE=OD-OE=OB-OE=x+2-4=x-2,
所以S△OBD=
OB2,S△OCA=
OA2,S△DEF=
DE2,
所以y=S△OBD-S△OCA-S△DEF=
OB2-
OA2-
DE2=
(x+2)2-
x2-
(x-2)2=-
x2+2
x=-
(x-4)2+4
,
所以当x=4时,y有最大值,最大值为4
.

解:
(1)①因为MN平行x轴,所以P点的纵坐标为2
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
②由对称的性质可知O、C、D三点在一条直线上,连接OC,
因为tan∠POB=
2
| ||
| 6 |
| ||
| 3 |
设MN交CD于点E,则CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OME中,cos∠EOM=
| OM |
| OE |
| ||
| 2 |
2
| ||
| x+1 |
| ||
| 2 |
故答案为:3;
(2)在Rt△OME中,cos∠EOM=
| OM |
| OE |
| ||
| 2 |
分两种情况:当CE=2ED时,可知CE=
| 4 |
| 3 |
| 4 |
| 3 |
2
| ||
x+
|
| ||
| 2 |
| 2 |
| 3 |
当CE=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
2
| ||
x+
|
| ||
| 2 |
| 1 |
| 3 |
综上可知x的值为2
| 2 |
| 3 |
| 1 |
| 3 |
(3)存在,最大值为4
| 3 |
设MN交BD于点F,由(1)可知∠COA=60°,且OC=OA,OD=AB,所以△OAC和△OBD都为等边三角形,
又因为MN平行x轴,所以△DEF也为等边三角形,
在RtRt△OME中,可求得OE=4,且OA=x,OB=x+2,所以DE=OD-OE=OB-OE=x+2-4=x-2,
所以S△OBD=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
所以y=S△OBD-S△OCA-S△DEF=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| 3 |
| ||
| 4 |
| 3 |
所以当x=4时,y有最大值,最大值为4
| 3 |
点评:本题主要考查一次函数与对称的性质的应用,在(1)(2)中用x表示出CE的长度是解题的关键,在(3)中同上条件得出△OCA、△DEF、△ODB都是正三角形是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
观察图形:将一张长方形纸片对折,可得到一条折痕.继续对折,对折是每次折痕与上次折痕保持平行,那么对折8次后折痕的条数是( )


| A、16 | B、64 |
| C、128 | D、255 |
点A、B、C在一条直线上,线段AB=6cm,BC=4cm,则线段AC=( )
| A、10cm | B、2cm |
| C、10cm或2cm | D、不能确定 |
在△ABC中,AB=9,AC=40,BC=41,则该三角形为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |
 如图,在四边形ABCD中,AB=CD,点MN分别是边AD、BC的中点,O是BD的中点.求证:OM=ON.
如图,在四边形ABCD中,AB=CD,点MN分别是边AD、BC的中点,O是BD的中点.求证:OM=ON.