题目内容
8.若x1,x2是方程x2-2x-2012=0的两个实根,则代数式x12+2x1•x2-2x1的值为( )| A. | 0 | B. | -2012 | C. | 2012 | D. | 4024 |
分析 先根据根与系数的关系得出x1+x2=2,x1•x2=-2012,再由x2-2x-2012=0得出x12=2x1+2012,代入原式进行计算即可.
解答 解:∵x1,x2是方程x2-2x-2012=0的两个实根,
∴x1+x2=2,x1•x2=-2012,x12=2x1+2012,
∴原式=2x1+2012+2x1•x2-2x1
=2012+2x1•x2
=2012+2×(-2012)
=-2012.
故选B.
点评 此题考查了一元二次方程根与系数的关系的知识,注意若二次项系数不为1,x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,掌握根与系数的关系是解此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.二次函数y=a(x+k)2+k,无论k为何实数,其图象的顶点都在( )
| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
13.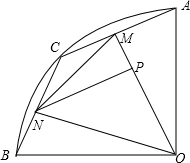 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )| A. | 随C点的运动而变化,NP的取值范围是1≤NP≤$\sqrt{2}$ | |
| B. | 随C点的运动而变化,最大值为$\frac{3\sqrt{2}}{2}$ | |
| C. | 等于$\sqrt{2}$ | |
| D. | 随C点的运动而变化,没有最值 |
18.有四条线段长度为3cm,4cm,5cm,6cm,从中任意取三条线段能组成三角形的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
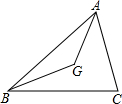 已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.