题目内容
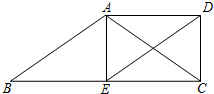如图，在梯形ABCD中，AD∥BC，点E是BC的中点，连接AC，DE，AC=AB，DE∥AB．求证：四边形AECD是矩形．考点：矩形的判定
专题：证明题
分析：先判断四边形AECD为平行四边形，然后由∠AEC=90°即可判断出四边形AECD是矩形．
解答：证明：∵AD∥BC，DE∥AB，
∴四边形ABED是平行四边形．
∴AD=BE．
∵点E是BC的中点，
∴EC=BE=AD．
∴四边形AECD是平行四边形．
∵AB=AC，点E是BC的中点，
∴AE⊥BC，即∠AEC=90°．
∴?AECD是矩形．
∴四边形ABED是平行四边形．
∴AD=BE．
∵点E是BC的中点，
∴EC=BE=AD．
∴四边形AECD是平行四边形．
∵AB=AC，点E是BC的中点，
∴AE⊥BC，即∠AEC=90°．
∴?AECD是矩形．
点评：本题考查了梯形和矩形的判定，难度适中，解题关键是掌握平行四边形和矩形的判定定理．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
下列说法正确的是（ ）
| A、1的立方根是±1 | ||
B、
| ||
C、
| ||
D、
|
下列事件中，属于不可能事件的是（ ）
| A、某两个数的和小于0 |
| B、某个数的相反数等于它本身 |
| C、某个数的绝对值小于0 |
| D、某两个负数的积大于0 |
下列说法正确的是（ ）
| A、射线是直线的一半 |
| B、延长直线AB到C |
| C、延长射线AB到C |
| D、直线上两个点和它们之间的部分叫做线段 |
（1）计算：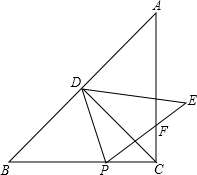
在Rt△ABC中，∠ACB=90°，AC=BC，D为AB边的中点，点P为BC边上一点，把△PBD沿PD翻折，点B落在点E处，设PE交AC于F，连接CD