题目内容
 已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠DAC=∠FEB.
已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠DAC=∠FEB.(1)求证:EF∥AC;
(2)若CA平分∠BCD,∠B=50°,∠D=120°,求∠BFE的度数.
考点:平行线的判定与性质
专题:计算题
分析:(1)由AD与BC平行,利用两直线平行内错角相等得到一对角相等,再由已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由AD与BC平行,利用两直线平行同旁内角互补,求出∠BCD的度数,由CA为角平分线求出∠ACB的度数,进而确定出∠FEB的度数,即可求出∠BFE的度数.
(2)由AD与BC平行,利用两直线平行同旁内角互补,求出∠BCD的度数,由CA为角平分线求出∠ACB的度数,进而确定出∠FEB的度数,即可求出∠BFE的度数.
解答:(1)证明:∵AD∥BC,
∴∠DAC=∠ACB,
∵∠DAC=∠FEB,
∴∠ACB=∠FEB,
∴EF∥AC;
(2)解:∵AD∥BC,
∴∠D+∠DCB=180°,
∵∠D=120°,
∴∠DCB=60°,
∵AC平分∠BCD,
∴∠ACB=∠ACD=30°,
∵EF∥AC,
∴∠FEB=∠ACD=30°,
∴∠BFE=180°-(∠B+∠FEB)=100°.
∴∠DAC=∠ACB,
∵∠DAC=∠FEB,
∴∠ACB=∠FEB,
∴EF∥AC;
(2)解:∵AD∥BC,
∴∠D+∠DCB=180°,
∵∠D=120°,
∴∠DCB=60°,
∵AC平分∠BCD,
∴∠ACB=∠ACD=30°,
∵EF∥AC,
∴∠FEB=∠ACD=30°,
∴∠BFE=180°-(∠B+∠FEB)=100°.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
下列语句正确的是( )
| A、在所有连接两点的线中,直线最短 |
| B、线段AB是点A与点B的距离 |
| C、在同一平面内,两条不重合的直线,不平行必相交 |
| D、三条直线两两相交,必定有三个交点 |
若∠A与∠B互补,且∠A>∠B,则∠B的余角是( )
A、
| ||
B、
| ||
C、
| ||
D、∠A-
|
 如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )| A、80° | B、100° |
| C、108° | D、110° |
下列说法正确的是( )
| A、射线是直线的一半 |
| B、延长直线AB到C |
| C、延长射线AB到C |
| D、直线上两个点和它们之间的部分叫做线段 |
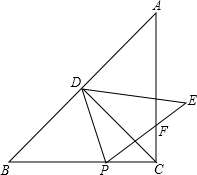 在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD
在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD 为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题:
为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题: