题目内容
已知在△ABC中,AD⊥BC于点D,点E,F,G分别是边BC,AB,AC的中点,求证:∠FEG=∠FDG=∠BAC.
考点:三角形中位线定理,直角三角形斜边上的中线,平行四边形的判定与性质
专题:证明题
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得GE∥AB,FE∥AC,然后判断出四边形AFEG是平行四边形,根据平行四边形的对角相等可得∠FEG=∠BAC,再根据直角三角形斜边上的中线等于斜边的一半DF=AF,DG=AG,根据等边对等角可得∠FDA=∠FAD,∠GDA=∠GAD,然后求出∠FDG=∠BAC,再等量代换即可得证.
解答: 证明:∵E,F,G分别是边BC,AB,AC的中点,
证明:∵E,F,G分别是边BC,AB,AC的中点,
∴GE∥AB,FE∥AC(三角形中位线定理),
∴四边形AFEG是平行四边形,
∴∠FEG=∠BAC,
又∵AD垂直于BC于点D,
∴∠ADB=∠ADC=90°,
∵F,G分别是AB,AC的中点,
∴DF=AF,DG=AG(直角三角形中,斜边上的中线等于斜边的一半),
∴∠FDA=∠FAD,∠GDA=∠GAD,
∴∠FDA+∠GDA=∠FAD+∠GAD,
即:∠FDG=∠BAC,
∴∠FEG=∠FDG=∠BAC.
 证明:∵E,F,G分别是边BC,AB,AC的中点,
证明:∵E,F,G分别是边BC,AB,AC的中点,∴GE∥AB,FE∥AC(三角形中位线定理),
∴四边形AFEG是平行四边形,
∴∠FEG=∠BAC,
又∵AD垂直于BC于点D,
∴∠ADB=∠ADC=90°,
∵F,G分别是AB,AC的中点,
∴DF=AF,DG=AG(直角三角形中,斜边上的中线等于斜边的一半),
∴∠FDA=∠FAD,∠GDA=∠GAD,
∴∠FDA+∠GDA=∠FAD+∠GAD,
即:∠FDG=∠BAC,
∴∠FEG=∠FDG=∠BAC.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的性质判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质是解题的关键,作出图形更形象直观.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
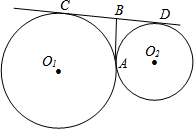 半径为9cm的⊙O1和半径为4cm的⊙O2外切于点A,直线CD和和⊙O1、⊙O2分别切于C、D两点,过A的直线和⊙O1相切于A点并和直线交于B点,则CD=
半径为9cm的⊙O1和半径为4cm的⊙O2外切于点A,直线CD和和⊙O1、⊙O2分别切于C、D两点,过A的直线和⊙O1相切于A点并和直线交于B点,则CD=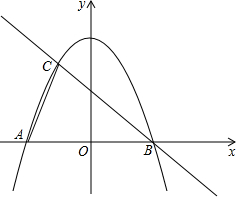 如图,抛物线y=
如图,抛物线y=