题目内容
12.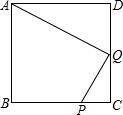 如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.
如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.(1)求证:△ADQ∽△QCP;
(2)已知∠QPC=55°,求∠QAD的度数.
分析 (1)由正方形ABCD中,BP=3PC,Q是CD的中点,易得CP:DQ=CQ:DA=1:2,∠C=∠D=90°,继而证得△ADQ∽△QCP;
(2)由△ADQ∽△QCP,根据相似的对应角相等,求得答案.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠C=∠D=90°,
∵BP=3PC,Q是CD的中点,
∴CP=$\frac{1}{4}$BC,CQ=DQ=$\frac{1}{2}$CD,
∴CP:DQ=CQ:DA=1:2,
∴△ADQ∽△QCP;
(2)解:∵∠C=90°,∠QPC=55°,
∴∠CQP=90°-∠QPC=35°,
∵△ADQ∽△QCP,
∴∠QAD=CQP=35°.
点评 此题考查了相似三角形的判定与性质以及正方形的性质.注意有两边对应成比例且夹角相等三角形相似.

练习册系列答案
相关题目
17.分式$\frac{ab}{2xy}$,$\frac{a}{3x{y}^{2}}$,$\frac{b}{4y}$的最简公分母是( )
| A. | 12xy2 | B. | 24x2y2 | C. | ab | D. | 12xy |
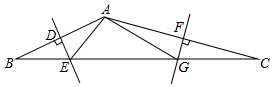 如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7.
如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.则△AEG的周长为7. 如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.
如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.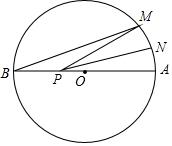 如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )
如图,AB是⊙O的直径,AB=6,点M在⊙O上,∠MBA=20°,N是$\widehat{MA}$的中点,P是直径AB上的一动点,若AN=1,则△PMN周长的最小值为( )