题目内容
4. 如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.
如图,在△ABC中,∠CAB=90°,AC=AB,过点A的直线交BC于点M,过点C作CD⊥AM,垂足为D,过点B作BE⊥AM,垂足为E,请你在图中找出一对全等三角形,并说明理由.
分析 根据余角的性质得到∠ACD=∠BAE,根据全等三角形的判定即可得到结论.
解答 解: △CAD≌△ABE,
△CAD≌△ABE,
理由:∵∠CAB=90°,
∴∠CAD+∠BAE=90°,
∵CD⊥AM,
∴∠CDA=90°,
∴∠ACD+∠DAC=90°,
∴∠ACD=∠BAE,
∵BE⊥AM,
∴∠AEB=90°,
在△CAD与△ABE中,$\left\{\begin{array}{l}{∠ACD=∠BAE}\\{∠CDA=∠AEB}\\{AC=AB}\end{array}\right.$,
∴△CAD≌△ABE.
点评 本题考查了全等三角形的判定,直角三角形的性质,熟练正确全等三角形的判定定理是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
14.计算(-2a)2•a3,正确的是( )
| A. | 2a5 | B. | -4a5 | C. | 4a5 | D. | 4a6 |
15.在线段AB上取一点C,使AC=$\frac{1}{3}$AB,再在线段AB的延长线上取一点D,使DB=$\frac{1}{4}$AD,则线段BC的长度是线段DC长度的( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
19.$\sqrt{32}$的整数部分是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16. 如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
 如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )
如图,点A,B,C在⊙O上,若∠C=35°,则∠AOB=( )| A. | 17.5° | B. | 35° | C. | 60° | D. | 70° |
13.如果a的倒数是-1,那么a2016=( )
| A. | 1 | B. | -1 | C. | 2016 | D. | -2016 |
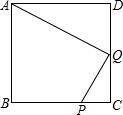 如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.
如图:正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点.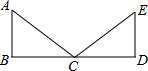 如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD).
如图,AB⊥BD,AB∥ED,AC=EC,要证明△ABC≌△EDC,若以“AAS”为依据,还要添加一个条件为∠A=∠E(或∠ACB=∠ECD).