题目内容
 已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=
已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=| 1 |
| 2 |
(1)求a的值;
(2)求一次函数y=kx+b的表达式;
(3)在同一坐标系中,画出这两个函数的图象,并求这两条直线与y轴围成的三角形的面积.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)把(2,a)代入正比例函数解析式即可得到a的值;
(2)把(-1,-5)、(2,1)代入y=kx+b中可得关于k、b的方程组,然后解方程组求出k、b即可;
(3)先利用描点法画哈图象,再求出两直线与y轴的交点坐标,然后根据三角形面积公式求解.
(2)把(-1,-5)、(2,1)代入y=kx+b中可得关于k、b的方程组,然后解方程组求出k、b即可;
(3)先利用描点法画哈图象,再求出两直线与y轴的交点坐标,然后根据三角形面积公式求解.
解答: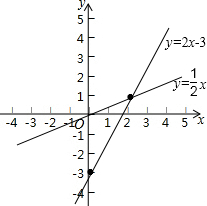 解:(1)把(2,a)代入y=
解:(1)把(2,a)代入y=
x得a=1;
(2)把(-1,-5)、(2,1)代入y=kx+b得
,
解得
,
所以一次函数解析式为y=2x-3;
(3)如图,
直线y=2x-3与y轴的交点坐标为(0,-3),直线y=
x与y轴的交点为原点,
这两条直线与y轴围成的三角形的面积=
×3×2=3.
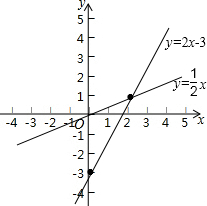 解:(1)把(2,a)代入y=
解:(1)把(2,a)代入y=| 1 |
| 2 |
(2)把(-1,-5)、(2,1)代入y=kx+b得
|
解得
|
所以一次函数解析式为y=2x-3;
(3)如图,
直线y=2x-3与y轴的交点坐标为(0,-3),直线y=
| 1 |
| 2 |
这两条直线与y轴围成的三角形的面积=
| 1 |
| 2 |
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α
已知线段a,b,∠α,求作:△ABC,AB=a,AC=b,∠BAC=∠α 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)? 如图,点P是等边三角形ABC内一点,PA=1,PB=
如图,点P是等边三角形ABC内一点,PA=1,PB=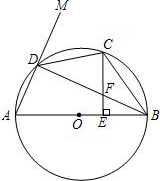 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
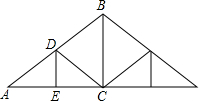 如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长?
如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长?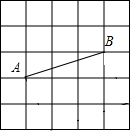 在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形.
在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形. 如图,在△ABC中,∠B=∠C,D为边BC上一点,E为AC上一点,∠BAD=50°,∠ADE=∠AED,求∠EDC的度数.
如图,在△ABC中,∠B=∠C,D为边BC上一点,E为AC上一点,∠BAD=50°,∠ADE=∠AED,求∠EDC的度数.