题目内容
1.已知关于x的方程$\frac{3x+n}{2x+1}$=2的解是非正数,则n的取值范围是n≤2且n$≠\frac{3}{2}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,根据分式方程解是非负数列出不等式,求出不等式的解集即可得到m的范围.
解答 解:去分母,得3x+n=2(2x+1),
解得:x=n-2,
∵x≤0,2x+1≠0,
∴n-2≤0,x≠-$\frac{1}{2}$,
∴n≤2,n-2≠-$\frac{1}{2}$,
∴n≠$\frac{3}{2}$,
∴n≤2且n≠$\frac{3}{2}$.
故答案为:$n≤2且n≠\frac{3}{2}$.
点评 此题考查了分式方程的解,解决本题的关键是根据分式方程解是非负数列出不等式,注意在任何时候都要考虑分母不为0.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9.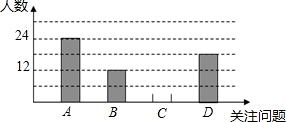 6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:
根据表中提供的信息解答以下问题:
(1)表中的a=60,b=0.4;
(2)请将条形统计图补充完整;
(3)如果小明所在的学校有4200名学生,那么根据小明提供的信息估计该校关注“全球变暖”的学生大约有多少人?
 6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:| 关注问题 | 频数 | 频率 |
| A | 24 | b |
| B | 12 | 0.2 |
| C | n | 0.1 |
| D | 18 | m |
| 合计 | a | 1 |
(1)表中的a=60,b=0.4;
(2)请将条形统计图补充完整;
(3)如果小明所在的学校有4200名学生,那么根据小明提供的信息估计该校关注“全球变暖”的学生大约有多少人?
 如图,函数y=2x和y=ax+5的图象相交于A(m,3),则不等式0<2x<ax+5的解集为0<x<$\frac{3}{2}$.
如图,函数y=2x和y=ax+5的图象相交于A(m,3),则不等式0<2x<ax+5的解集为0<x<$\frac{3}{2}$.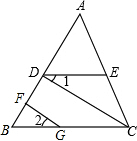 已知,如图,CD⊥AB,GF⊥AB,∠1=∠2,试说明:∠B=∠ADE.
已知,如图,CD⊥AB,GF⊥AB,∠1=∠2,试说明:∠B=∠ADE.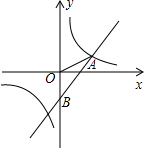 如图,已知在平面直角坐标系中,O是坐标原点,点A(3,1)是反比例函数y1=$\frac{k}{x}$与一次函数y2=x+b的交点,点B是一次函数与y轴的交点.
如图,已知在平面直角坐标系中,O是坐标原点,点A(3,1)是反比例函数y1=$\frac{k}{x}$与一次函数y2=x+b的交点,点B是一次函数与y轴的交点.
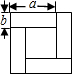 用4张全等的长方形拼成一个如图所示的正方形,利用面积的不同表示方法可以写出一个代数恒等式.若长方形的长和宽分别为a、b,则该图可表示的代数恒等式是4ab=(a+b)2-(a-b)2..
用4张全等的长方形拼成一个如图所示的正方形,利用面积的不同表示方法可以写出一个代数恒等式.若长方形的长和宽分别为a、b,则该图可表示的代数恒等式是4ab=(a+b)2-(a-b)2..