题目内容
6.设非零实数x满足条件:$\left\{\begin{array}{l}x+{(-1)^n}<3x-3×{(-1)^n}\\ \frac{1}{2}(x-4)<\frac{1}{3}(x-4)\end{array}\right.$(n是自然数),求$\frac{1}{x}$的取值范围.分析 先将原不等式进行化简,再分x为偶数与奇数两种情况进行讨论.
解答 解:原不等式组可化为$\left\{\begin{array}{l}x>2×{(-1)^n}\\ x<4.\end{array}\right.$,解得2×(-1)n<x<4(n是自然数),
当n为偶数时,解得2<x<4,
所以$\frac{1}{4}$<$\frac{1}{x}$<$\frac{1}{2}$;
当n为奇数时,解得-2<x<4(x≠0),
所以$\frac{1}{x}$<-$\frac{1}{2}$或$\frac{1}{x}$>$\frac{1}{4}$.
点评 本题考查的是解一元一次不等式组,在解答此题时要进行分类讨论,不要漏解.

练习册系列答案
相关题目
16.5的相反数是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
14.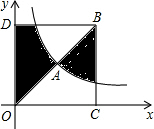 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )| A. | 23 | B. | 18 | C. | 11 | D. | 8 |
15.分解因式2x3-18x结果正确的是( )
| A. | 2x(x+3)2 | B. | 2x(x-3)2 | C. | 2x(x2-9) | D. | 2x(x+3)(x-3) |