题目内容
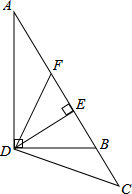 在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=
在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=| 1 |
| 5 |
考点:相似三角形的判定与性质
专题:
分析:根据直角三角形的性质求出DF=BF=
λ;根据勾股定理列出关于BC、λ的方程组,解方程组即可解决问题.
| 5 |
| 2 |
解答: 解:如图,∵BE=
解:如图,∵BE=
AB,
∴设BE=λ,则AB=5λ;
∵点F为直角△ABD的中点,
∴DF=BF=
λ;
∵DF⊥CD,
∴△BDF为直角三角形,
由勾股定理得:CF2=CD2+DF2,
即(
+CB)2=(
)2+22①;
由射影定理得:DE2=AE•BE=4λ2;
由勾股定理得:22=4λ2+(λ+BC)2②
联立①②并解得:BC=
.
故答案为
.
 解:如图,∵BE=
解:如图,∵BE=| 1 |
| 5 |
∴设BE=λ,则AB=5λ;
∵点F为直角△ABD的中点,
∴DF=BF=
| 5 |
| 2 |
∵DF⊥CD,
∴△BDF为直角三角形,
由勾股定理得:CF2=CD2+DF2,
即(
| 5λ |
| 2 |
| 5λ |
| 2 |
由射影定理得:DE2=AE•BE=4λ2;
由勾股定理得:22=4λ2+(λ+BC)2②
联立①②并解得:BC=
| 8 |
| 13 |
故答案为
| 8 |
| 13 |
点评:该题以直角三角形为载体,以勾股定理、射影定理等几何知识点的考查为核心构造而成;对运算求解能力、推理探究能力等均提出了较高的要求.

练习册系列答案
相关题目

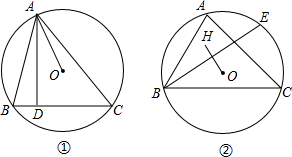 如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.
如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.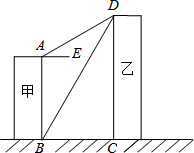 如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.
如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD. 小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明) 如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm.
如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm. 如图是游乐园的一角.
如图是游乐园的一角.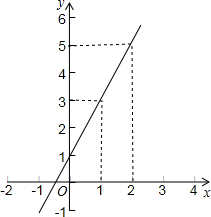 小明认为一次函数y=kx+b中,x每增加1,kx增加了k,b没有变,因此y也增加了k.如图所示的一次函数图象中,x从1变到2时,函数值从3变到5,增加了2,因此该一次函数中k的值是2.请你用待定系数法验证小明的说法.
小明认为一次函数y=kx+b中,x每增加1,kx增加了k,b没有变,因此y也增加了k.如图所示的一次函数图象中,x从1变到2时,函数值从3变到5,增加了2,因此该一次函数中k的值是2.请你用待定系数法验证小明的说法.