题目内容
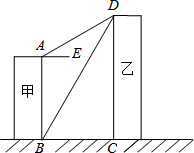 如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.
如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.考点:解直角三角形的应用
专题:
分析:根据题意结合等腰三角形的性质得出∠ADB=30°,进而求出AD=AB=36,再求出DH的长即可得出答案.
解答: 解:延长AE交DC于点H,
解:延长AE交DC于点H,
∵AB⊥BC,DC⊥BC,∠DBC=60°,∠DAE=30°,
∴∠ABC=∠DCB=90°,∠ABD=∠ABC-∠DBC=30°,
∵AE∥BC,∴∠DHA=90°,∠DEH=60°,
∴∠ADB=30°,
在△ABD中,故AD=AB=36,
在Rt△ADH中,∠DAH=30°,
故DH=
AD=18,
则CD=CH+DH=36+18=54.
 解:延长AE交DC于点H,
解:延长AE交DC于点H,∵AB⊥BC,DC⊥BC,∠DBC=60°,∠DAE=30°,
∴∠ABC=∠DCB=90°,∠ABD=∠ABC-∠DBC=30°,
∵AE∥BC,∴∠DHA=90°,∠DEH=60°,
∴∠ADB=30°,
在△ABD中,故AD=AB=36,
在Rt△ADH中,∠DAH=30°,
故DH=
| 1 |
| 2 |
则CD=CH+DH=36+18=54.
点评:此题主要考查了解直角三角形的应用,得出DH的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,∠1的两边分别为
如图,∠1的两边分别为
 已知如图,请根据图形回答问题.
已知如图,请根据图形回答问题.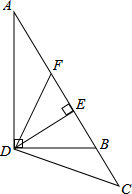 在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=
在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE= 如图是由几个小正方体块所搭几何体的俯视图,小正方体中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图是由几个小正方体块所搭几何体的俯视图,小正方体中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.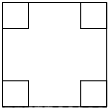 如图,面积为48cm2的正方形纸板四个角是面积为3cm2的小正方形,现将四个小正方形剪掉,制作一个无盖的长方体盒子.
如图,面积为48cm2的正方形纸板四个角是面积为3cm2的小正方形,现将四个小正方形剪掉,制作一个无盖的长方体盒子.