题目内容
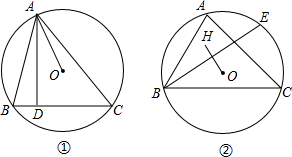 如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.
如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.(1)请你帮小聪证明这个结论;
(2)运用以上结论解决问题:如图②,H为△ABC的垂心,若∠ABC的平分线BE⊥HO,⊙O的半径为10,求弦AC的长.
考点:圆周角定理
专题:计算题
分析:(1)作直径AE,连结CE,如图①,根据圆周角定理得到∠ACE=90°,∠AEC=∠ABD,然后利用等角的余角相等即可得到结论;
(2)作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,根据圆周角定理得∠CBF=∠CAF=90°,再根据垂心的定义得AH⊥BC,BH⊥AC,则AF∥BH,AH⊥BF,于是可判断四边形AHBF为平行四边形,得到AF=BH;接着由∠ABE=∠CBE,∠ABH=∠CBO得到∠HOE=∠OBE,加上OH⊥BE,所以△BOH为等腰三角形,得到BH=OB=10,则AF=10,然后在Rt△AFC中,利用勾股定理计算AC的长.
(2)作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,根据圆周角定理得∠CBF=∠CAF=90°,再根据垂心的定义得AH⊥BC,BH⊥AC,则AF∥BH,AH⊥BF,于是可判断四边形AHBF为平行四边形,得到AF=BH;接着由∠ABE=∠CBE,∠ABH=∠CBO得到∠HOE=∠OBE,加上OH⊥BE,所以△BOH为等腰三角形,得到BH=OB=10,则AF=10,然后在Rt△AFC中,利用勾股定理计算AC的长.
解答:(1)证明: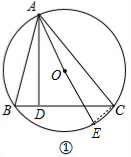 作直径AE,连结CE,如图①,
作直径AE,连结CE,如图①,
∵AE为直径,
∴∠ACE=90°,
∵AD⊥BC,
∴∠ADB=90°,
∵∠AEC=∠ABD,
∴∠BAD=∠EAC,即∠BAD=∠OAC;
(2)解: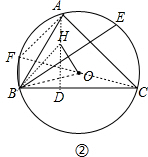 作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,
作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,
∵CF为直径,
∴∠CBF=∠CAF=90°,
∵AH⊥BC,BH⊥AC,
∴AF∥BH,AH⊥BF,
∴四边形AHBF为平行四边形,
∴AF=BH,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
由(1)的结论得∠ABH=∠CBO,
∴∠HOE=∠OBE,
∵OH⊥BE,
∴△BOH为等腰三角形,
∴BH=OB=10,
∴AF=BH=10,
在Rt△AFC中,∵CF=20,AF=10,
∴AC=
=10
.
 作直径AE,连结CE,如图①,
作直径AE,连结CE,如图①,∵AE为直径,
∴∠ACE=90°,
∵AD⊥BC,
∴∠ADB=90°,
∵∠AEC=∠ABD,
∴∠BAD=∠EAC,即∠BAD=∠OAC;
(2)解:
 作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,
作直径CF,延长AH交BC于D,连结AF、BF、BH、OB,如图②,∵CF为直径,
∴∠CBF=∠CAF=90°,
∵AH⊥BC,BH⊥AC,
∴AF∥BH,AH⊥BF,
∴四边形AHBF为平行四边形,
∴AF=BH,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
由(1)的结论得∠ABH=∠CBO,
∴∠HOE=∠OBE,
∵OH⊥BE,
∴△BOH为等腰三角形,
∴BH=OB=10,
∴AF=BH=10,
在Rt△AFC中,∵CF=20,AF=10,
∴AC=
| FC2-AF2 |
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了平行四边形的判定与性质和等腰三角形的判定与性质.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,把一张长方形纸片沿AB折叠后,若∠1=50°,则∠2的度数为
如图,把一张长方形纸片沿AB折叠后,若∠1=50°,则∠2的度数为
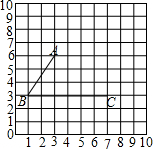 已知如图,请根据图形回答问题.
已知如图,请根据图形回答问题.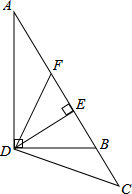 在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=
在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=