题目内容
 如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D,若∠D=20°,则∠A=
如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D,若∠D=20°,则∠A=考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义及三角形的外角性质可表示出∠A与∠D,从而不难发现两者的数量关系,进一步得出答案即可.
解答:
解:∵∠ABC的平分线交∠ACE的外角平分线∠ACE的平分线于点D,
∴∠ABC=2∠DBC,∠ACE=2∠DCE,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE-∠DBE,
∵∠ACE是△ABC的外角,
∠A=∠ACE-∠ABC=2∠DCE-2∠DBE=2(∠DCE-∠DBE),
∴∠A=2∠D=40°.
故答案为:40°.
∴∠ABC=2∠DBC,∠ACE=2∠DCE,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE-∠DBE,
∵∠ACE是△ABC的外角,
∠A=∠ACE-∠ABC=2∠DCE-2∠DBE=2(∠DCE-∠DBE),
∴∠A=2∠D=40°.
故答案为:40°.
点评:此题主要考查角平分线的意义以及三角形的外角的性质:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
对于分式
,永远成立的是( )
| 1 |
| x-1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列给出的方程中,不是二元一次方程的是( )
| A、2x-2y=3 | ||
B、
| ||
C、
| ||
D、
|
 用小立方体搭成的几何体的主视图和俯视图如图,问:这样的几何体是否只有一种?它最少需多少个立方体?它最多需多少个立方体?请画出最多与最少时的左视图.
用小立方体搭成的几何体的主视图和俯视图如图,问:这样的几何体是否只有一种?它最少需多少个立方体?它最多需多少个立方体?请画出最多与最少时的左视图.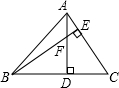 已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.
已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.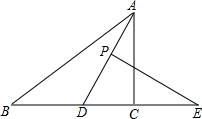 在△ABC中,AD平分角∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
在△ABC中,AD平分角∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E. 如图,在△ABC中,∠CAB=45°,∠1=∠2=∠3
如图,在△ABC中,∠CAB=45°,∠1=∠2=∠3 如图所示,已知∠1=115°,∠2=50°,∠3=65°,EG为∠NEB的平分线,那么AB∥CD,EG∥FH吗?
如图所示,已知∠1=115°,∠2=50°,∠3=65°,EG为∠NEB的平分线,那么AB∥CD,EG∥FH吗?