题目内容
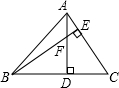 已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.
已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.考点:含30度角的直角三角形
专题:证明题
分析:由BE⊥AC于点E,可得:∠AEF=90°,由∠EAD=30°,可得:AF=2EF,然后由AF=DF,可得DF=2EF,由AD⊥BC于点D,可得∠BDF=90°,由对顶角相等可得:∠AFE=∠BFD,然后根据三角形内角和为180°,即可求出∠FBD=30°,进而可得BF=2FD=4EF.
解答:
证明:∵BE⊥AC于点E,
∴∠AEF=90°,
∵∠EAD=30°,
∴AF=2EF,
∵AF=DF,
∴DF=2EF,
∵AD⊥BC于点D,
∴∠BDF=90°,
∵∠AFE=∠BFD,且∠EAD+∠AFE+∠AEF=∠FBD+∠BDF+∠BFD=180°,
∴∠FBD=30°,
∴BF=2FD=4EF,
即BF=4EF.
∴∠AEF=90°,
∵∠EAD=30°,
∴AF=2EF,
∵AF=DF,
∴DF=2EF,
∵AD⊥BC于点D,
∴∠BDF=90°,
∵∠AFE=∠BFD,且∠EAD+∠AFE+∠AEF=∠FBD+∠BDF+∠BFD=180°,
∴∠FBD=30°,
∴BF=2FD=4EF,
即BF=4EF.
点评:此题考查了含30°角的直角三角形的性质,熟记30°角所对的直角边等于斜边的一半,是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 一次函数y=mx+n的图象如图所示,则方程mx+n=0的解为( )
一次函数y=mx+n的图象如图所示,则方程mx+n=0的解为( )| A、x=2 | B、y=2 |
| C、x=-3 | D、y=-3 |
如图都是由同样大小的正三角形按一定的规律组成的,其中第1个图形共有1个正三角形,第2个图形中共有5个正三角形,第3个图形中共有13个正三角形…,按照此规律第5个图形中正三角形的个数为( )


| A、25 | B、45 | C、48 | D、60 |
计算36m÷6m的结果为( )
| A、6 |
| B、30 |
| C、6m |
| D、30m |

 如图,在△ABC中,AC=2,∠A=45°,tanB=
如图,在△ABC中,AC=2,∠A=45°,tanB= 5个棱长为1的正方体组成如图所示的几何体.
5个棱长为1的正方体组成如图所示的几何体. 如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D,若∠D=20°,则∠A=
如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D,若∠D=20°,则∠A=