题目内容
如图，A，B，C，D四点都在⊙O上，AD是⊙O的直径，若AD=10，AC=6，AB=8，求BC边上的高．考点：相似三角形的判定与性质,圆周角定理
专题：
分析：如图，作辅助线；证明△ABD∽△AEC，列出比例式，即可解决问题．
解答：
解：如图，过点A作AE⊥BC；连接BD；
则∠D=∠C；
∵AD为⊙O的直径，
∴∠ABD=90°，∠ABD=∠AEC；
∴△ABD∽△AEC，
∴AB：AE=AD：AC，而AD=10，AC=6，AB=8，
∴AE=4.8．
即BC边上的高为4.8．
解：如图，过点A作AE⊥BC；连接BD；则∠D=∠C；
∵AD为⊙O的直径，
∴∠ABD=90°，∠ABD=∠AEC；
∴△ABD∽△AEC，
∴AB：AE=AD：AC，而AD=10，AC=6，AB=8，
∴AE=4.8．
即BC边上的高为4.8．
点评：该题主要考查了圆周角定理及其推论、相似三角形的判定及其性质等知识点的应用问题；作辅助线，构造相似三角形是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图，在四边形ABCD中，AD∥BC，AB=BC=3BE，CE=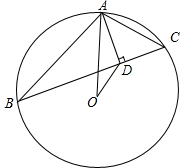
已知⊙O是△ABC的外接圆，AD⊥BC于D，连结AO．
如图，等腰△ABC中，AB=AC，D是BC上一点，且AD=BD．
按照下列要求完成作图及相应的问题解答