题目内容
为规范学生的在校表现,某班实行了操行评分制,根据学生的操行分高低分为A、B、C、D四个等
级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为 人,得到等级A的学生人数在扇形统计图中的圆心角度数是 ;
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操
行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽
到的代表中有小伟或小颖的概率.
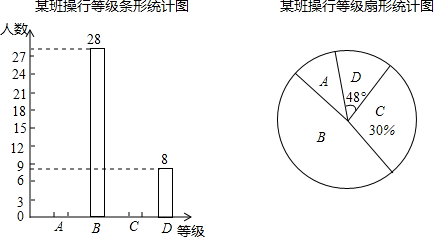
级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操
行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽
到的代表中有小伟或小颖的概率.

考点:条形统计图,扇形统计图,列表法与树状图法
专题:
分析:(1)该班的总人数=D级人数÷对应的百分比,得到等级A的学生人数在扇形统计图中的圆心角度数=
×360°,
(2)利用A,C能的人数补全条形统计图;
(3)一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,即可得出P(小伟或小颖)=
.
| 得到等级A的学生人数 |
| 总人数 |
(2)利用A,C能的人数补全条形统计图;
(3)一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,即可得出P(小伟或小颖)=
| 5 |
| 8 |
解答:解:(1)该班的总人数为8÷
=60(人),
得到等级A的学生人数为60-28-8-60×30%=6(人)
得到等级A的学生人数在扇形统计图中的圆心角度数是
×360°=36°,
故答案为:60,36°.
(2)如图,
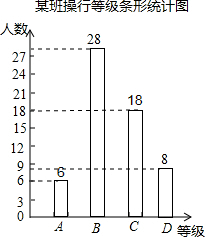
(3)得A的总人数为6人,其中2男4女,假设男1为小伟,女1为小颖.

一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,
所以,P(小伟或小颖)=
.
| 48 |
| 360 |
得到等级A的学生人数为60-28-8-60×30%=6(人)
得到等级A的学生人数在扇形统计图中的圆心角度数是
| 6 |
| 60 |
故答案为:60,36°.
(2)如图,

(3)得A的总人数为6人,其中2男4女,假设男1为小伟,女1为小颖.

一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,
所以,P(小伟或小颖)=
| 5 |
| 8 |
点评:本题主要考查了条形统计图,圆形统计图及树形图列举法,解题的关键是概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
下列等式变形正确的是( )
A、如果s=vt,那么v=
| ||
B、如果
| ||
| C、如果x-3=y-3,那么x=y | ||
| D、如果a=b,那么a+b=b-a |
 如图,△ABC中,AD、BE分别是BC、AC 边上的高,EB、AD的延长线交于F点,且AC=BF.求证:AD=BD.
如图,△ABC中,AD、BE分别是BC、AC 边上的高,EB、AD的延长线交于F点,且AC=BF.求证:AD=BD. 如图,P为正比例函数y=
如图,P为正比例函数y= 如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.
如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.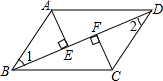 完成下面的证明过程:
完成下面的证明过程: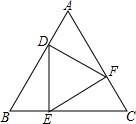 如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为
如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为 如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=25°,则∠EBF的度数是
如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=25°,则∠EBF的度数是