题目内容
6．
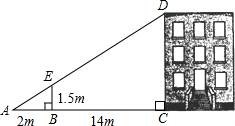如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2cm，BC=14m，则楼高CD为（ ）m．| A． | 10.5 | B． | 12 | C． | 13 | D． | 15 |
分析 先根据题意得出△ABE∽△ACD，再根据相似三角形的对应边成比例即可求出CD的值．
解答 解：∵EB⊥AC，DC⊥AC，
∴EB∥DC，
∴△ABE∽△ACD，
∴$\frac{BE}{CD}$=$\frac{AB}{AC}$，
∵BE=1.5，AB=2，BC=14，
∴AC=16，
∴$\frac{1.5}{CD}$=$\frac{2}{16}$，
∴CD=12．
故选B．
点评 本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例的性质是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．如图，已知点E，D，F分别为△ABC三边上的点，下列条件中能判断EF∥BC的是（ ）
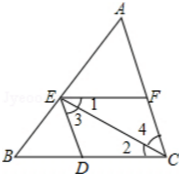
| A． | ∠1=∠3 | B． | ∠3=∠A | C． | ∠1=∠2 | D． | ∠1=∠A |
11．
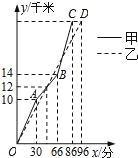在一次自行车越野赛中，甲乙两名选手行驶的路程y（千米）随时间x（分）变化的图象（全程）如图，根据图象判定下列结论不正确的是（ ）
在一次自行车越野赛中，甲乙两名选手行驶的路程y（千米）随时间x（分）变化的图象（全程）如图，根据图象判定下列结论不正确的是（ ）| A． | 前30分钟，甲在乙的前面 | B． | 这次比赛的全程是28千米 | ||
| C． | 第48分钟时，两人第一次相遇 | D． | 甲先到达终点 |
18．已知点（3，-1）是y=$\frac{k}{x}$（k≠0）双曲线上的一点，则下列各点在该双曲线上的是（ ）
| A． | （1，3） | B． | （-1，-3） | C． | （-1，3） | D． | （3，1） |
15．
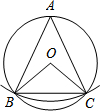如图，AB是⊙O的弦（AB不是直径），以点A为圆心，以AB长为半径画弧交⊙O于点C，连结AC、BC、OB、OC．若∠ABC=65°，则∠BOC的度数是（ ）
如图，AB是⊙O的弦（AB不是直径），以点A为圆心，以AB长为半径画弧交⊙O于点C，连结AC、BC、OB、OC．若∠ABC=65°，则∠BOC的度数是（ ）| A． | 50° | B． | 65° | C． | 100° | D． | 130° |