题目内容
13．在Rt△ABC中，∠C=90°，∠B=60°，b=3$\sqrt{3}$，求a、c与∠A．分析 在Rt△ABC中，由∠C=90°，∠B=60°，得到∠A=30°，根据tanA=$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$，求得a，然后由直角三角形的性质得到c=2a=6．
解答 解：在Rt△ABC中，∠C=90°，∠B=60°，
∴∠A=30°，
∴tanA=$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$，
∵b=3$\sqrt{3}$，
∴a=3，
∴c=2a=6．
点评 本题考查的是解直角三角形，题目中告诉的是一条直角边和斜边，用勾股定理可以求出另一条直角边．得到是一等腰直角三角形，然后确定两个直角的度数．
练习册系列答案
相关题目
如图，依图填空：
2．
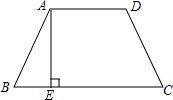如图所示，在梯形ABCD中，∠ABC=60°，AB=CD=AD，过点A作AE⊥BC于点E，AE=3，CE=3$\sqrt{3}$，则梯形ABCD的周长与面积分别是（ ）
如图所示，在梯形ABCD中，∠ABC=60°，AB=CD=AD，过点A作AE⊥BC于点E，AE=3，CE=3$\sqrt{3}$，则梯形ABCD的周长与面积分别是（ ）| A． | 8，9$\sqrt{3}$ | B． | 10$\sqrt{3}$，9$\sqrt{3}$ | C． | 9$\sqrt{3}$，10$\sqrt{3}$ | D． | 8$\sqrt{3}$，9$\sqrt{3}$ |