题目内容
14.解不等式组:$\left\{\begin{array}{l}{2x-1<7}\\{\frac{3x-1}{2}-1≥x}\end{array}\right.$,并在数轴上表示出不等式组的解集.分析 分别解两个不等式得到x<4和x≥3,则可根据大小小大中间找确定不等式组的解集,然后利用数轴表示解集.
解答 解:$\left\{\begin{array}{l}{2x-1<7①}\\{\frac{3x-1}{2}-1≥x②}\end{array}\right.$,
解①得x<4,
解②得x≥3,
所以不等式组的解集为3≤x<4,
用数轴表示为:
点评 本题考查了一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
2.现有两根木棒,它们的长分别是20cm和30cm.若要订一个三角架,则下列四根木棒的长度应选( )
| A. | 10cm | B. | 30cm | C. | 50cm | D. | 70cm |
19.某校研究性学习小组在学习二次根式$\sqrt{{a}^{2}}$=|a|之后,研究了如下四个问题,其中错误的是( )
| A. | 在a>1的条件下化简代数式a+$\sqrt{{a}^{2}-2a+1}$的结果为2a-1 | |
| B. | 当a+$\sqrt{{a}^{2}-2a+1}$的值恒为定值时,字母a的取值范围是a≤1 | |
| C. | a+$\sqrt{{a}^{2}-2a+1}$的值随a变化而变化,当a取某个数值时,上述代数式的值可以为$\frac{1}{2}$ | |
| D. | 若$\sqrt{{a}^{2}-2a+1}$=($\sqrt{a-1}$)2,则字母a必须满足a≥1 |
4.下列因式分解完全正确的是( )
| A. | -2a2+4a=-2a(a+2) | B. | -4x2-y2=-(2x+y)2 | ||
| C. | a2-8ab+16b2=(a+4b)2 | D. | 2x2+xy-y2=(2x-y)(x+y) |
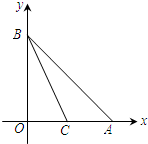 如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC. 已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.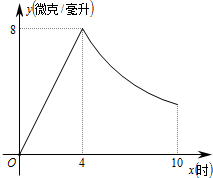 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).