题目内容
20. 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角45°的三角形如图放置,使三角形斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角45°的三角形如图放置,使三角形斜边的两个端点分别与A、D重合,E为直角顶点,连接EC、BE(1)延长CE、BA交于F,设BE与AC相交于点O,则OE与EF的关系应为OE=EF,OE⊥EF;
(2)在(1)的条件下,已知AF=2,AO=1,求AB的长.
分析 (1)由题意可知△EAB≌△EDC得BE=EC,∠AEB=∠DEC,进而可以证明∠BEC=90°,然后证明△BEF≌△CEO即可解决问题.
(2)由(1)可知BF=OC,设AB=x则BF=x+2,OC=2x-1,故x+2=2x-1解方程即可.
解答 (1)结论OE=EF,OE⊥EF.理由如下:
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=$\frac{1}{2}$AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中,
$\left\{\begin{array}{l}{AE=DE}\\{∠EAB=∠EDC}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴BE⊥EC,
∵∠F+∠ACF=90°,∠F+∠FBE=90°,
∴∠FBE=∠OCE,
在△BEF和△CEO中,
$\left\{\begin{array}{l}{∠FBE=∠ECO}\\{∠BEF=∠OEC}\\{BE=CE}\end{array}\right.$,
∴△BEF≌△CEO,
∴OE=EF,OE⊥EF.
(2)由(1)可知△BEF≌△CEO,
∴BF=CO,设AB=x,则AC=2x,BF=x+2,OC=2x-1,
∴x+2=2x-1,
∴x=3,
∴AB=3.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质,解题的关键是用了两次全等,学会用方程的思想解决问题,属于中考常考题型.

 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )| A. | 28° | B. | 42° | C. | 56° | D. | 70° |
 如图,已知AB=AC,AD=AE,∠1=∠3,那么∠E=∠D吗?为什么?
如图,已知AB=AC,AD=AE,∠1=∠3,那么∠E=∠D吗?为什么?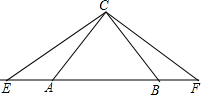 如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积.
如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积. 如图,扇形AOB的圆心角为60°,四边形OCDE是边长为1的菱形,点C、E、D分别在OA、OB和弧AB上,若过B作BF∥ED交CD的延长线于点F,则图中阴影部分的面积为$\frac{π-\sqrt{3}}{2}$.
如图,扇形AOB的圆心角为60°,四边形OCDE是边长为1的菱形,点C、E、D分别在OA、OB和弧AB上,若过B作BF∥ED交CD的延长线于点F,则图中阴影部分的面积为$\frac{π-\sqrt{3}}{2}$.