Question

9．如图，扇形AOB的圆心角为60°，四边形OCDE是边长为1的菱形，点C、E、D分别在OA、OB和弧AB上，若过B作BF∥ED交CD的延长线于点F，则图中阴影部分的面积为$\frac{π-\sqrt{3}}{2}$．

Answer 1

分析 连接OD、CE，两线交于M，求出OD和CE长，从图中可看出阴影部分的面积=扇形面积-菱形的面积．然后依面积公式计算即可．

解答 解：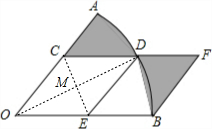
连接OD、CE，两线交于M，
∵四边形OCDE是菱形，
∴OC=1，CE⊥OD，OD=2OM，CE=2CM，∠COM=$\frac{1}{2}$∠AOB=$\frac{1}{2}×60°$=30°，
∴CM=$\frac{1}{2}$OC=$\frac{1}{2}×1$=$\frac{1}{2}$，OM=$\frac{\sqrt{3}}{2}$，
∴OD=2OM=$\sqrt{3}$，EC=2CM=1，
∵BF∥ED，BE∥DF，
∴四边形DEBF是平行四边形，
∴DF=BE，BF=DE，
在△DFB和△BED中
$\left\{\begin{array}{l}{DF=BE}\\{DB=DB}\\{BF=DE}\end{array}\right.$
∴△DFB≌△BED，
∴S_△DFB=S_△DBE，
∴图中阴影部分的面积S=S_扇形AOB-S_菱形OCDE=$\frac{60π×（\sqrt{3}）^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{π-\sqrt{3}}{2}$，
故答案为：$\frac{π-\sqrt{3}}{2}$．

点评 本题考查了菱形的性质，勾股定理，扇形的面积的应用，利用割补法把不规则图形转化成规则图形求解的能力，再把阴影部分的面积转化为扇形的面积和菱形的面积求解．