题目内容
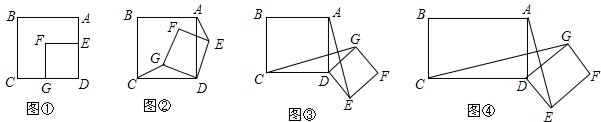
3.正方形ABCD和正方形DEFG如图①放置,保持正方形ABCD不动,将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<180°)(1)当0°<α<90°时,如图②,连结AE、CG,则AE:CG=1;
(2)当90°<α<180°时,如图③,连结AE、CG,(1)中的结论还成立吗?请说明理由;
(3)将图③中的正方形ABCD和正方形DEFG分别改为矩形ABCD和矩形DEFG,且使AD=4,CD=6,ED=2,GD=3,如图④,求AE:CG的值.
分析 (1)证明△ADE≌△CDE即可证得;
(2)同(1)可证明△ADE≌△CDE即可证得;
(3)证明△CDG∽△ADE,据此即可求解.
解答 解:(1)在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠CDG=∠ADE}\\{DG=DE}\end{array}\right.$,
∴△ADE≌△CDE,
∴AE=CG,
∴AE:CG=1;
(2)结论仍成立.
理由是:
在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠CDG=∠ADE}\\{DG=DE}\end{array}\right.$,
∴△ADE≌△CDE,
∴AE=CG,
∴AE:CG=1;
(3)∵AD=4,CD=6,ED=2,GD=3,
∴$\frac{CD}{AD}=\frac{DG}{DE}$,
又∵∠CDG=∠ADE,
∴△CDG∽△ADE,
∴$\frac{AE}{CG}=\frac{AD}{CD}$=$\frac{4}{6}$=$\frac{2}{3}$.
点评 本题考查了全等三角形的判定与性质以及相似三角形的判定与性质,根据旋转的性质注意到∠ADE=∠CDG是本题的关键.

练习册系列答案
相关题目
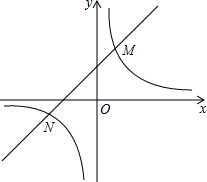 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M(1,3),N两点,点N的横坐标为-3.
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M(1,3),N两点,点N的横坐标为-3.
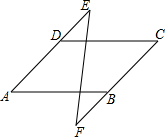 如图,已知AB∥CD,∠A=∠C,那么∠E=∠F吗?为什么?
如图,已知AB∥CD,∠A=∠C,那么∠E=∠F吗?为什么?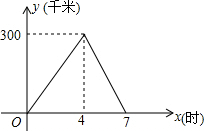 小李从甲地前往乙地,到达乙地后立刻返回,设小李与甲地相距y(千米),离开甲地的时间为x(时),y与x之间的函数图象如图所示.
小李从甲地前往乙地,到达乙地后立刻返回,设小李与甲地相距y(千米),离开甲地的时间为x(时),y与x之间的函数图象如图所示.