题目内容
2.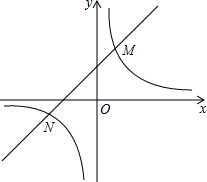 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M(1,3),N两点,点N的横坐标为-3.
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M(1,3),N两点,点N的横坐标为-3.(1)根据图象信息可得关于x的方程$\frac{m}{x}$=kx+b的解为1或-3;
(2)求一次函数的解析式.
分析 (1)根据图象可知方程$\frac{m}{x}$=kx+b的解即为一次函数图象在反比例函数图象交点的横坐标,结合M、N点的横坐标可得出答案.
(2)首先把点于M(1,3)代入y=$\frac{m}{x}$,求出m的值,因为点N的横坐标为-3,所以可代入反比例函数的解析式求出其纵坐标,再把M,N的坐标代入一次函数的解析式求出k和b的值即可.
解答 解:(1)根据图象可知方程$\frac{m}{x}$=kx+b的解即为一次函数图象在反比例函数图象交点的横坐标,
∵点M的横坐标为1,点N的横坐标为-3,
∴关于x的方程$\frac{m}{x}$=kx+b的解为1或-3,
故答案为:1或-3;
(2)∵反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M(1,3),
∴m=3,
∴y=$\frac{3}{x}$,
∵点N的横坐标为-3,
∴点N的纵坐标为-1.,
把M,N的坐标代入y=kx+b得
$\left\{\begin{array}{l}{3=k+b}\\{-1=-3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴y=x+2.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式,解题的关键是先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
13.下列运算正确的是( )
| A. | a+2a=2a2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | (x-3)2=x2-9 | D. | (x2)3=x6 |
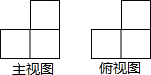 某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体( )
某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体( )