题目内容
13.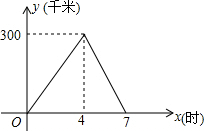 小李从甲地前往乙地,到达乙地后立刻返回,设小李与甲地相距y(千米),离开甲地的时间为x(时),y与x之间的函数图象如图所示.
小李从甲地前往乙地,到达乙地后立刻返回,设小李与甲地相距y(千米),离开甲地的时间为x(时),y与x之间的函数图象如图所示.(1)求小李从甲地前往乙地过程中y与x之间的函数关系式.
(2)求小李从乙地返回甲地过程中y与x之间的函数关系式.
(3)直接写出小李距乙地100千米时x的值.
分析 (1)设小李从甲地前往乙地过程中y与x之间的函数关系式为y=k1x,利用待定系数法解答即可;
(2)设小李从乙地返回甲地过程中y与x之间的函数关系式为y=k2x+b,利用待定系数法解答即可;
(3)小李距乙地100千米,则距甲地300-100=200米,再把y=200分别代入两个解析式解答即可.
解答 解:(1)设小李从甲地前往乙地过程中y与x之间的函数关系式为y=k1x,
∵图象经过(4,300),
∴300=4k1,
∴k1=75,
∴y=75x;
(2)设小李从乙地返回甲地过程中y与x之间的函数关系式为y=k2x+b,
∵图象经过(4,300)、(7,0),
∴$\left\{\begin{array}{l}{4{k}_{2}+b=300}\\{7{k}_{2}+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=-100}\\{b=700}\end{array}\right.$,
∴y=-100x+700;
(3)因为小李距乙地100千米,则距甲地300-100=200米,
把y=200代入y=75x中,200=75x,
解得:x=$\frac{8}{3}$,
把y=200代入y=-100x+700中,200=-100x+700,
解得:x=5.
点评 此题考查一次函数的应用,关键是列出解析式利用待定系数法解出解析式.

练习册系列答案
相关题目
1. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′位置,且CC′∥AB,则∠CAB′的度数是( )| A. | 30° | B. | 45° | C. | 40° | D. | 50° |
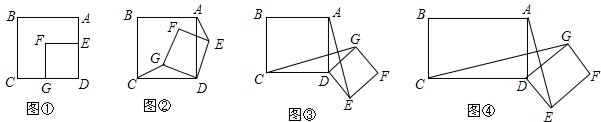
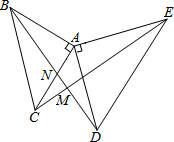 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.

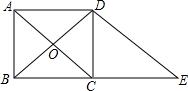 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作DE∥AC,交BC的延长线于点E.求证:BD=DE.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点D作DE∥AC,交BC的延长线于点E.求证:BD=DE.