题目内容
14.填空并解答:(1)方程x2+2x+1=0的根为x1=-1,x2=-1,x1+x2=-2,x1x2=1.
(2)方程x2-3x-4=0的根为x1=4,x2=-1,x1+x2=3,x1x2=-4.
(3)方程3x2+4x+1=0的根为x1=$-\frac{1}{3}$,x2=-1,x1+x2=$-\frac{4}{3}$,x1x2=$\frac{1}{3}$.
(4)由(1)(2)(3)你能得出什么猜想?你能证明你的猜想吗?
分析 (1)首先利用配方法解方程,求得方程的两个解,即可求得两根的和与积;
(2)利用因式分解法可得结果;
(3)利用求根公式,即可求得方程的两个根,进而求得两个根的和与积.
(4)观察方程的两根的和与积与方程的系数之间的关系,利用系数表示出两个根的和与积即可得到结论.
解答 解:(1)x2+2x+1=0
即(x+1)2=0
∴x+1=0
∴x=-1
∴x1=-1,x2=-1,x1+x2=-2,x1x2=1;
故答案为:-1,-1,-2,1;
(2)∵x2-3x-4=0,
∴(x-4)(x+1)=0
∴x1=4,x2=-1,x1+x2=3,x1x2=-4;
故答案为:4,-1,3,-4;
(3)x=$\frac{-4±\sqrt{{4}^{2}-4×3×1}}{6}$=$\frac{-4±2}{6}$
∴x1=$-\frac{1}{3}$,x2=-1,x1+x2=-$\frac{4}{3}$,x1x2=$\frac{1}{3}$.
故答案为:$-\frac{1}{3}$,-1,$-\frac{4}{3}$,$\frac{1}{3}$;
(4)结论:若方程ax2+bx+c=0(a≠0,a、b、c是常数,x是未知数)有两个根x1、x2,
则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.
点评 本题考查了一元二次方程的解法,以及一元二次方程的根与系数之间的关系,关键是正确求得方程的解.

练习册系列答案
相关题目
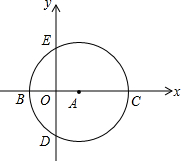 如图,在直角坐标系中,以点A(3,0)为圆心,以5为半径作圆与x轴相交于点B,C,与y轴相交于点D,E.
如图,在直角坐标系中,以点A(3,0)为圆心,以5为半径作圆与x轴相交于点B,C,与y轴相交于点D,E.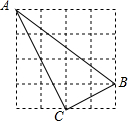 如图:正方形网格中每个小方格的边长为1,且点A、B、C均为格点.
如图:正方形网格中每个小方格的边长为1,且点A、B、C均为格点.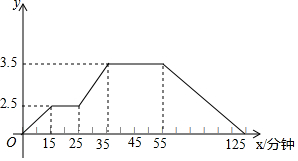 如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.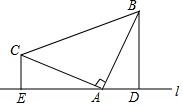 已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线L的垂线段BD、CE,垂足分别D、E.
已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线L的垂线段BD、CE,垂足分别D、E.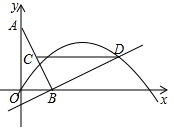 如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.