题目内容
20.若有理数a满足$\root{3}{1-{a}^{2}}=1-{a}^{2}$,$\sqrt{1-\frac{1}{3}b}=0$,求$\root{b}{a}$的值.分析 利用立方根等于本身的数为0,-1,1,求出a的值,由算术平方根的定义求出b的值,即可确定出原式的值.
解答 解:根据$\root{3}{1-{a}^{2}}$=1-a2,得:1-a2=0或1-a2=-1或1-a2=-1,
解得:a=±1,0,±$\sqrt{2}$,
根据$\sqrt{1-\frac{1}{3}b}$=0,得到1-$\frac{1}{3}$b=0,即b=3,
当a=1时,原式=1;当a=-1时,原式=-1;当a=0时,原式=0;当a=$\sqrt{2}$时,原式=$\root{6}{2}$;当a=-$\sqrt{2}$时,原式=-$\root{6}{2}$.
点评 此题考查了立方根,算术平方根,熟练的各自的定义是解本题的关键.

练习册系列答案
相关题目
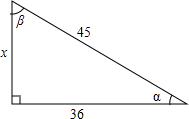 如图,分别求∠α和∠β的正弦、余弦和正切.
如图,分别求∠α和∠β的正弦、余弦和正切. 如图,求阴影部分的面积.
如图,求阴影部分的面积.