题目内容
11. 如图,为测悬崖的高AB,某小组在平地点C处测得点B在北偏西60°方向.沿正西方向行走50m,在点D处测得点B在北偏西45°方向,并测得点A的仰角为60°.求悬崖的高.(若有根号不用取近似值.AB为竖直方向,B,C,D在同一水平面.)
如图,为测悬崖的高AB,某小组在平地点C处测得点B在北偏西60°方向.沿正西方向行走50m,在点D处测得点B在北偏西45°方向,并测得点A的仰角为60°.求悬崖的高.(若有根号不用取近似值.AB为竖直方向,B,C,D在同一水平面.)
分析 先作BE⊥CD于E,设BE=DE=x,根据CE=DE+CD,得到$\sqrt{3}$x=x+50,求得BE=DE=25($\sqrt{3}$+1),BD=$\sqrt{2}$x=25($\sqrt{6}$+$\sqrt{2}$),在Rt△ABD中,根据∠ADB=60°,即可得到AB=BD×tan60°,据此可得AB的长.
解答 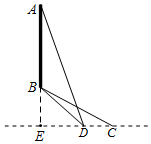 解:如图,作BE⊥CD于E,
解:如图,作BE⊥CD于E,
由题可得,∠BDE=45°,∠BCE=30°,CD=50,
∴BE=DE,
设BE=DE=x,
Rt△BCE中,CE=$\frac{BE}{tan30°}$=$\sqrt{3}$x,
∵CE=DE+CD,
∴$\sqrt{3}$x=x+50,
解得x=25($\sqrt{3}$+1),
∴BE=DE=25($\sqrt{3}$+1),
∴Rt△BDE中,BD=$\sqrt{2}$x=25($\sqrt{6}$+$\sqrt{2}$),
∵在Rt△ABD中,∠ADB=60°,
∴AB=BD×tan60°=$\sqrt{3}$BD=25(3$\sqrt{2}$+$\sqrt{6}$)=75$\sqrt{2}$+25$\sqrt{6}$,
∴悬崖的高AB为(75$\sqrt{2}$+25$\sqrt{6}$)米.
点评 本题主要考查了解直角三角形的应用,解决问题的关键是作辅助线构造直角三角形,解题时注意:所画的示意图为立体图形,△ABD为直角三角形且∠ABD=90°,∠ADB为仰角.

练习册系列答案
相关题目
19.下列各数中最小的是( )
| A. | |-5| | B. | -23 | C. | -(+3) | D. | $\sqrt{16}$ |
1.将九年级两个班男生掷实心球的成绩进行整理,并绘制出频数分布表、扇形统计图和频数分布直方图(不完整).(x表示成绩,且规定x≥6.25合格,x≥9.25为优秀)
(1)频数分布表中,a=5,b=15,其中成绩合格的有45人,请补全频数分布直方图;
(2)这两个班男生成绩的中位数落在C组,扇形统计图中E组对应的圆心角是36°;
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,用列表法或画树状图法求甲、乙两位同学至少有1人被选中的概率(提示:成绩优秀的其他同学可用a、b、c、d、e…表示)

| 组别 | 成绩(米) | 频数 |
| A | 5.25≤x<6.25 | 5 |
| B | 6.25≤x<7.25 | 10 |
| C | 7.25≤x<8.25 | a |
| D | 8.25≤x<9.25 | 15 |
| E | 9.25≤x≤10.25 | b |
(2)这两个班男生成绩的中位数落在C组,扇形统计图中E组对应的圆心角是36°;
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,用列表法或画树状图法求甲、乙两位同学至少有1人被选中的概率(提示:成绩优秀的其他同学可用a、b、c、d、e…表示)

 如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°.
如图,已知AB∥CF,DE∥CF,DE与BC交于点P,若∠ABC=70°,∠CDE=130°. 如图,二次函数y=ax2+bx-4$\sqrt{3}$的图象经过A(-1,0)、B(4,0)两点,于y轴交于点D.
如图,二次函数y=ax2+bx-4$\sqrt{3}$的图象经过A(-1,0)、B(4,0)两点,于y轴交于点D.