题目内容
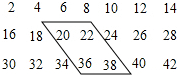 如图是由一些偶数排成的一个数阵.
如图是由一些偶数排成的一个数阵.(1)观察图中平行四边形框内的四个数,你发现它们有什么关系吗?
(2)在图中任意画一个类似图中已画出的平行四边形框,设其中左上角的那个数是x,请你用含x的式子表示出其它三个数;
(3)任意画出的平行四边形框内的四个数之和能为2014吗?如果能,请求出这四个数;若不能,请说明理由.
考点:一元一次方程的应用
专题:
分析:(1)根据已知数据直接得出答案;
(2)设第一个数为x,观察表中数据得到第二个数为x+2,第四个数为x+18,第三个数为x+16;
(3)可列方程x+x+2+x+16+x+18=2014,解得x=494.5,于是得到不存在这样的四个数,使它们的和为2014.
(2)设第一个数为x,观察表中数据得到第二个数为x+2,第四个数为x+18,第三个数为x+16;
(3)可列方程x+x+2+x+16+x+18=2014,解得x=494.5,于是得到不存在这样的四个数,使它们的和为2014.
解答:解:(1)由图可得:20+38=22+36,
20+2=22,20+16=36,22+16=38;
(2)设第一个数为x,则第二个数为x+2,第四个数为x+18,第三个数为x+16;
(2)不存在.理由如下:
设第一个数为x,则第二个数为x+2,第四个数为x+18,第三个数为x+16,
根据题意得x+x+2+x+16+x+18=2014,
解得x=494.5.
所以不存在这样的四个数,使它们的和为2014.
20+2=22,20+16=36,22+16=38;
(2)设第一个数为x,则第二个数为x+2,第四个数为x+18,第三个数为x+16;
(2)不存在.理由如下:
设第一个数为x,则第二个数为x+2,第四个数为x+18,第三个数为x+16,
根据题意得x+x+2+x+16+x+18=2014,
解得x=494.5.
所以不存在这样的四个数,使它们的和为2014.
点评:本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四边形ABCD中,∠A+∠B=120°,AD=BC,以CD为边向外作等边△CDE,连接AE,BE.求证:△ABE为等边三角形.
如图,在四边形ABCD中,∠A+∠B=120°,AD=BC,以CD为边向外作等边△CDE,连接AE,BE.求证:△ABE为等边三角形. 已知AB=AC,AD=AE,BD=CE,求证:∠ADE=∠EAC+∠ECA.
已知AB=AC,AD=AE,BD=CE,求证:∠ADE=∠EAC+∠ECA. 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.
如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE. 如图,直线l1:y=
如图,直线l1:y=