题目内容
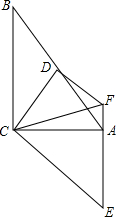 如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.
如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.(1)若AC=6,BC=8,求CD的长;
(2)过点D作FD∥EC,交EA延长线于点F,连接CF,求证:EF+AF=BC.
考点:全等三角形的判定与性质
专题:
分析:(1)根据勾股定理可求得AB的长,再根据直角三角形斜边中线是斜边一半可以求得CD的长;
(2)延长FD交BC于点G,易证△ADF≌△BDG和△CFG≌△FCA,可得AF=BG和EF=CG即可解题.
(2)延长FD交BC于点G,易证△ADF≌△BDG和△CFG≌△FCA,可得AF=BG和EF=CG即可解题.
解答:解:(1)∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=
=10,
∵点D为AB的中点,
∴CD=
AB=5;
(2)延长FD交BC于点G,
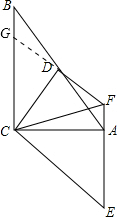
∵EF∥BC,
∴∠FAD=∠GBD,
在△ADF和△BDG中,
,
∴△ADF≌△BDG,(ASA)
∴AF=BG,
∵EF∥BC,DF∥CE,
∴∠CFE=∠BCF,∠CFD=∠FCE,
在△CFG和△FCA中,
,
∴△CFG≌△FCA(ASA),
∴EF=CG,
∵BC=BG+CG,
∴BC=EF+AF.
∴AB=
| BC2+AC2 |
∵点D为AB的中点,
∴CD=
| 1 |
| 2 |
(2)延长FD交BC于点G,

∵EF∥BC,
∴∠FAD=∠GBD,
在△ADF和△BDG中,
|
∴△ADF≌△BDG,(ASA)
∴AF=BG,
∵EF∥BC,DF∥CE,
∴∠CFE=∠BCF,∠CFD=∠FCE,
在△CFG和△FCA中,
|
∴△CFG≌△FCA(ASA),
∴EF=CG,
∵BC=BG+CG,
∴BC=EF+AF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了斜边中线是斜边一半的性质,本题中求证△ADF≌△BDG和△CFG≌△FCA是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.
如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.
 如图,直线l1:y=
如图,直线l1:y=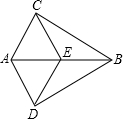 如图,已知∠ACB=∠ADB=90°,AC=AD,E在AB上,连接CE、DE
如图,已知∠ACB=∠ADB=90°,AC=AD,E在AB上,连接CE、DE