题目内容
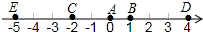 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,(1)移动1次后该点到原点的距离为
(2)移动2次后该点,到原点的距离为
(3)移动3次后该点到原点的距离为
(4)试问移动n次后该点到原点的距离为多少个单位长度?
考点:数轴
专题:规律型
分析:根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式就可解决问题.
解答:解:由题意可得:移动1次后该点对应的数为0+1=1,到原点的距离为1;
移动2次后该点对应的数为1-3=-2,到原点的距离为2;
移动3次后该点对应的数为-2+6=4,到原点的距离为4;
∴移动奇数次后该点到原点的距离为
;
移动偶数次后该点到原点的距离为
.
故答案为1,2,4.
移动2次后该点对应的数为1-3=-2,到原点的距离为2;
移动3次后该点对应的数为-2+6=4,到原点的距离为4;
∴移动奇数次后该点到原点的距离为
| 3n-1 |
| 2 |
移动偶数次后该点到原点的距离为
| 3n-2 |
| 2 |
故答案为1,2,4.
点评:本题考查了数轴,以及用正负数可以表示具有相反意义的量,还考查了数轴上点的坐标变化和平移规律(左减右加),考查了一列数的规律探究.对这列数的奇数项、偶数项分别进行探究是解决这道题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
小惠在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示-3的点重合,若数轴上A、B两点之间的距离为2014(A在B的左侧),且A、B两点经上述折叠后重合,则A点表示的数为( )
| A、-1006 |
| B、-1007 |
| C、-1008 |
| D、-1009 |
 如图,直线l1:y=
如图,直线l1:y=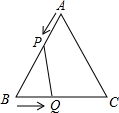 已知:如图所示,△ABC是边长6cm等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t s
已知:如图所示,△ABC是边长6cm等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t s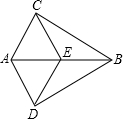 如图,已知∠ACB=∠ADB=90°,AC=AD,E在AB上,连接CE、DE
如图,已知∠ACB=∠ADB=90°,AC=AD,E在AB上,连接CE、DE