题目内容
9.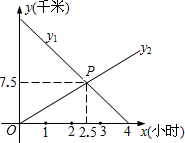 小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.
小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.(1)试用文字说明交点P表示的实际意义;
(2)求AB两地间的距离;
(3)小东和小明谁先到达目的地?他比对方早到了多长时间?
分析 (1)因为小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,所以交点P(2.5,7.5)的意义是经过2.5小时后,小东与小明在距离B地7.5千米处相遇;
(2)需求直线y1的解析式,因为它过点(2.5,7.5),(4,0),利用待定系数法即可求出其解析式.然后令x=0,求出此时的y值即可;
(3)求出y2的解析式,当y=20时,求出x的值,即可解答.
解答 解:(1)交点P所表示的实际意义是:经过2.5小时后,小东与小明在距离B地7.5千米处相遇.
(2)设y1=kx+b(k≠0),
又∵y1经过点P(2.5,7.5),(4,0),
∴$\left\{\begin{array}{l}{2.5k+b=7.5}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-5}\\{b=20}\end{array}\right.$,
∴y1=-5x+20,
当x=0时,y1=20,
故AB两地之间的距离为20千米.
(3)设y2=k2x(k2≠0),
把(2.5,7.5)代入y2=k2x得:2.5k2=7.5,
解得:k2=3,
则y2=3x,
当y2=20时,x=$\frac{20}{3}$,
∴小明到达目的地需要$\frac{20}{3}$小时,
而小东到达目的地需要4小时,
∴小东先到达目的地,
他比对方早到了:$\frac{20}{3}-4=\frac{8}{3}$(小时).
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法求一次函数的解析式.

练习册系列答案
相关题目
17.下列方程中,不是一元二次方程的是( )
| A. | x2=1 | B. | x(x-1)=x(x-2) | C. | x2+2=0 | D. | x(x-1)=x |
14.如果x<0,y<0,且3x-2y=$\sqrt{xy}$,则$\frac{x}{y}$的值为( )
| A. | -$\frac{4}{9}$ | B. | 1 | C. | $\frac{4}{9}$ | D. | 1或$\frac{4}{9}$ |
19.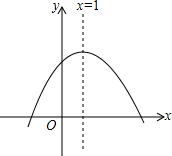 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | b<0 | ||
| C. | c>0 | D. | 方程ax2+bx+c=0有两个实数根 |
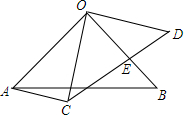 如图,已知△OAB和△0CD都是等腰直角三角形,点O是直角顶点,OA=10,OC=6$\sqrt{2}$,将△OCD绕点O旋转,使CD与OB相交于点E,当△BDE变成直角三角形时,线段AC的长为2或2$\sqrt{13}$.
如图,已知△OAB和△0CD都是等腰直角三角形,点O是直角顶点,OA=10,OC=6$\sqrt{2}$,将△OCD绕点O旋转,使CD与OB相交于点E,当△BDE变成直角三角形时,线段AC的长为2或2$\sqrt{13}$. 已知多项式m5n2-1中,含字母的项的系数为b,多项式的次数为c,常数项为a,请回答问题.
已知多项式m5n2-1中,含字母的项的系数为b,多项式的次数为c,常数项为a,请回答问题.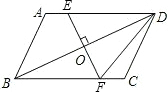 已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.
已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.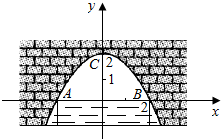 图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系: