题目内容
19.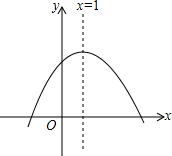 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | b<0 | ||
| C. | c>0 | D. | 方程ax2+bx+c=0有两个实数根 |
分析 根据抛物线的开口方向得出a的符号,抛物线的对称轴在y轴的右侧,a,b异号,得出b的符号,抛物线和y轴的交点在正半轴上得出c的符号,抛物线和x轴的交点个数得出方程ax2+bx+c=0根的情况.
解答 解:∵抛物线开口向下,
∴a<0,故A不合题意;
∵对称轴在y轴的右侧,a,b异号,
∴b>0,故B正确;
∵抛物线和y轴的正半轴相交,
∴c>0,故C不合题意;
∵抛物线和x轴有两个交点,
∴方程ax2+bx+c=0有两个不等实根,故D不合题意.
故选B.
点评 本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
10.下列实数中是无理数的是( )
| A. | 0.38 | B. | $\sqrt{4}$ | C. | -$\frac{22}{7}$ | D. | π |
7.已知关于x的方程,(1)ax2+bx+c=0;(2)1+(x+1)(x-1)=0;(3)x2-4x=8+x2;(4)(k2+1)x2+kx+1=0中,是一元二次方程的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列运算一定正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{{4}^{2}-{3}^{2}}$=1 | C. | ($\sqrt{-a}$)2=a | D. | $\sqrt{4{a}^{3}}$=2a$\sqrt{a}$ |
8.已知代数式x-2y的值是3,则代数式4y+1-2x的值是( )
| A. | -7 | B. | -5 | C. | -3 | D. | -1 |
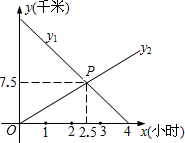 小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.
小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.