题目内容
18.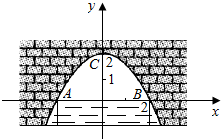 图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
分析 (1)设出抛物线的解析式,由图中点在抛物线上,用待定系数法求出抛物线解析式;
(2)把y=-1代入y=-$\frac{1}{2}$x2+2,即可得到结论.
解答 解:(1)设这条抛物线的解析式为y=ax2+bx+c(a≠0).
由已知抛物线经过点A(-2,0),B(2,0),C(0,2),
将三点坐标代入得:
$\left\{\begin{array}{l}{c=2}\\{4a+2b+c=0}\\{4a-2b+c=0}\end{array}\right.$
解得:a=-1,b=0,c=2,
故抛物线的解析式为y=-$\frac{1}{2}$x2+2.
(2)当y=-1时,即-$\frac{1}{2}$x2+2=-1,
解得:x=±$\sqrt{6}$,
故当水面下降1m时,则水面的宽度为2$\sqrt{6}$m.
点评 本题主要考查了用待定系数法求二次函数的解析式,根据图中信息得出函数经过的点的坐标是解题的关键.

练习册系列答案
相关题目
10.下列实数中是无理数的是( )
| A. | 0.38 | B. | $\sqrt{4}$ | C. | -$\frac{22}{7}$ | D. | π |
7.已知关于x的方程,(1)ax2+bx+c=0;(2)1+(x+1)(x-1)=0;(3)x2-4x=8+x2;(4)(k2+1)x2+kx+1=0中,是一元二次方程的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.已知代数式x-2y的值是3,则代数式4y+1-2x的值是( )
| A. | -7 | B. | -5 | C. | -3 | D. | -1 |
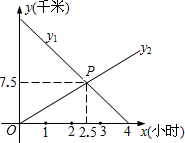 小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.
小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的线段y1,y2分别表示小东、小明离B地的距离y与所用的时间x的关系.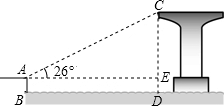 如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)
如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米) 如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
如图,已知一次函数y=-$\frac{1}{2}$x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.