题目内容
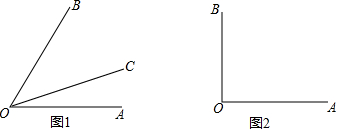
9. 某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示,根据图中的信息可知:免费托运行李质量应不超过19kg.
某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示,根据图中的信息可知:免费托运行李质量应不超过19kg.
分析 由函数图象由待定系数法可以直接求出函数的解析式;由题意得知免费托运,就是运费为0,当y=0代入求出函数的解析式就可以得出结论;
解答 解:设y与x之间的函数关系式为y=kx+b,由函数图象,得
$\left\{\begin{array}{l}{330=30k+b}\\{630=40k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=30}\\{b=-570}\end{array}\right.$,
∴y=30x-570(x>19),
由题意,得
当y=0时,x=19,
∴免费托运行李质量的范围是不超过19千克.
故答案为:19.
点评 本题考查了待定系数法求一次函数的解析式的运用,在解答本题时求出一次函数的解析式是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.设a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数,则a-b+c=( )
| A. | 1 | B. | 2 | C. | 0 | D. | 以上都不对 |
4.妈妈将2万元为小明存了一个6年期的教育储蓄(免利息税),6年后,总共能得27056元,则这种教育储蓄的年利率为( )
| A. | 5.86% | B. | 5.88% | C. | 5.84% | D. | 5.82% |
1.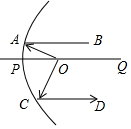 卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
 卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )| A. | 65° | B. | 75° | C. | 115° | D. | 135° |
18.点P(-1,2)关于y轴对称的点得坐标为( )
| A. | (1,-2) | B. | (-1,-2) | C. | (1,2) | D. | (2,-1) |
19.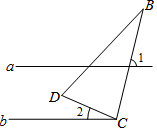 如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
 如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )| A. | 25° | B. | 15° | C. | 20° | D. | 30° |
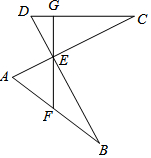 如图,AC,BD交于点E,AC⊥BD,BE=EC,∠B=∠C,过E作EG⊥DC,垂足为G,交AB于F点.
如图,AC,BD交于点E,AC⊥BD,BE=EC,∠B=∠C,过E作EG⊥DC,垂足为G,交AB于F点.