题目内容
6.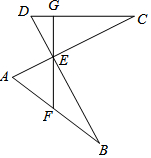 如图,AC,BD交于点E,AC⊥BD,BE=EC,∠B=∠C,过E作EG⊥DC,垂足为G,交AB于F点.
如图,AC,BD交于点E,AC⊥BD,BE=EC,∠B=∠C,过E作EG⊥DC,垂足为G,交AB于F点.求证:(1)△ABE≌△DCE;
(2)F为AB的中点.
分析 (1)根据全等三角形的判定定理即可得到结论;
(2)根据余角的性质得到∠D=∠GEC,根据全等三角形的性质得到∠D=∠A,等量代换得到∠A=∠AEF,求得AF=EF,根据等腰三角形的性质得到EF=BF,于是得到结论.
解答  证明:(1)在△ABE与△DCE中,$\left\{\begin{array}{l}{∠DEC=∠AEB=90°}\\{∠C=∠B}\\{BE=CE}\end{array}\right.$,
证明:(1)在△ABE与△DCE中,$\left\{\begin{array}{l}{∠DEC=∠AEB=90°}\\{∠C=∠B}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE;
(2)∵EG⊥DC,AC⊥BD,
∴∠DGE=∠DEC=90°,
∴∠D+∠DEG=∠DEG+∠GEC=90°,
∴∠D=∠GEC,
∵△ABE≌△DCE,
∴∠D=∠A,
∵∠AEF=∠GEC,
∴∠A=∠AEF,
∴AF=EF,
∵∠A+B=∠AEF+∠BEF=90°,
∴∠B=∠BEF,
∴EF=BF,
∴AF=BF,
∴F为AB的中点.
点评 本题考查了全等三角形的判定和性质,直角三角形的性质,等腰三角形的性质,熟练掌握全等三角形的判定是解题的关键.

练习册系列答案
相关题目
16.16平方根是( )
| A. | 4 | B. | -4 | C. | ±4 | D. | ±8 |
17.下列运算正确的是( )
| A. | $\sqrt{1\frac{4}{9}}$=1+$\frac{2}{3}$ | B. | (-2x2)3=-6x6 | C. | ($\frac{1}{2}$)-2=4 | D. | (x-1)2=x2-12 |
1.下列不等式的变形正确的是( )
| A. | 由a<b,得ac<bc | B. | 由ac<bc,得a<b | C. | 由a<b,得az2<bz2 | D. | 由az2<bz2,得a<b |
11.四边形ABCD的内角,∠A,∠B,∠C,∠D度数之比如下,则四边形是圆内接四边形的是( )
| A. | 4:2:2:5 | B. | 3:1:2:5 | C. | 4:1:1:5 | D. | 3:1:2:4 |
15. 如图,根据实数a,b,c,d在数轴上的位置,判断其中最大的数是( )
如图,根据实数a,b,c,d在数轴上的位置,判断其中最大的数是( )
 如图,根据实数a,b,c,d在数轴上的位置,判断其中最大的数是( )
如图,根据实数a,b,c,d在数轴上的位置,判断其中最大的数是( )| A. | a | B. | b | C. | c | D. | d |
 平行四边形是中心对称图形.如图,?ABCD以点O为旋转中心,按顺时针方向旋转180度后,与原来的图形能互相重合.
平行四边形是中心对称图形.如图,?ABCD以点O为旋转中心,按顺时针方向旋转180度后,与原来的图形能互相重合. 某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示,根据图中的信息可知:免费托运行李质量应不超过19kg.
某航空公司托运行李的费用y元与托运行李的质量x(kg)之间的函数关系如图所示,根据图中的信息可知:免费托运行李质量应不超过19kg.