题目内容
17. (1)已知a、b满足$\sqrt{2a+8}$+|b-$\sqrt{3}$|=0,解关于x的方程(a+2)x+b2=a-1.
(1)已知a、b满足$\sqrt{2a+8}$+|b-$\sqrt{3}$|=0,解关于x的方程(a+2)x+b2=a-1.(2)实数a,b在数轴上的位置如图所示,化简:|a-b|-$\sqrt{{a}^{2}}$.
分析 (1)先根据非负数的性质求出a,b的值,再代入方程求出x的值即可;
(2)根据各点在数轴上的位置判断出a、b的符号,再把原式进行化简即可.
解答 解:(1)∵a、b满足$\sqrt{2a+8}$+|b-$\sqrt{3}$|=0,
∴2a+8=0,b-$\sqrt{3}$=0,解得a=-4,b=$\sqrt{3}$,
∴原方程可化为-2x+3=-5,解得x=4.
(2)∵由图可知b<0<a,|b|>a,
∴a-b>0,
∴原式=a-b-a=-b.
点评 本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应关系是解答此题的关键.

练习册系列答案
相关题目
7.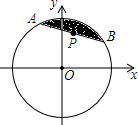 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
 如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )
如图,圆心在原点,半径为2的圆内有一点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),过点P作弦AB与劣弧AB组成一个弓形,则该弓形面积的最小值为( )| A. | π-1 | B. | π-2 | C. | $\frac{4π}{3}$-1 | D. | $\frac{4π}{3}$-$\sqrt{3}$ |
5.已知一元二次方程x2+0.1x-1=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法判断 |
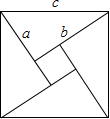 如图:这个图形被称为“弦图”,它是由四个全等的直角三角形拼成的正方形,你能用这个拼图验证勾股定理吗?
如图:这个图形被称为“弦图”,它是由四个全等的直角三角形拼成的正方形,你能用这个拼图验证勾股定理吗? 如图,在五角星ABCDE中,试说明:∠A+∠B+∠C+∠D+∠E=180°.
如图,在五角星ABCDE中,试说明:∠A+∠B+∠C+∠D+∠E=180°. 如图,操场上有两根旗杆间相距12m,小强同学从B点沿BA走向A,一定时间后他到达M点,此时他测得CM和DM的夹角为90°,且CM=DM,已知旗杆AC的高为3m,小强同学行走的速度为0.5m/s,则:
如图,操场上有两根旗杆间相距12m,小强同学从B点沿BA走向A,一定时间后他到达M点,此时他测得CM和DM的夹角为90°,且CM=DM,已知旗杆AC的高为3m,小强同学行走的速度为0.5m/s,则: