题目内容
20.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产x只熊猫的成本为R(元),售价每只为P(元),且R、P与x的关系式分别为R=500+30x,P=170-2x.(1)当日产量为多少时每日获得的利润为1750元?
(2)若可获得的最大利润为1950元,问日产量应为多少?
分析 (1)等量关系为:售价P×销售数量x-生产x只玩具熊猫的成本=1750,把相关数值代入求解即可.
(2)设每天所获利润为W,根据题意可表示出w与x的二次函数关系,再根据二次函数最值的求法,求得最值即可.
解答 解:(1)∵生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R,P与x的关系式分别为R=500+30x,
P=170-2x,
∴(170-2x)x-(500+30x)=1750,
解得 x1=25,x2=45(大于每日最高产量为40只,舍去).
解:(1)∵生产x只玩具熊猫的成本为R(元),售价每只为P(元),且R,P与x的关系式分别为R=500+30x,P=170-2x,
∴(170-2x)x-(500+30x)=1750,
解得 x1=25,x2=45(大于每日最高产量为40只,舍去).
(2)设每天所获利润为W,
由题意得,W=(170-2x)x-(500+30x)
=-2x2+140x-500
=-2(x2-70x)-500
=-2(x2-70x+352-352)-500
=-2(x2-70x+352)+2×352-500
=-2(x-35)2+1950.
当x=35时,W有最大值1950元.
答:当日产量为25只时,每日获得利润为1750元;要想获得最大利润,每天必须生产35个工艺品,最大利润为1950.
点评 此题考查了二次函数的应用,关键是得出等量关系:售价P×销售数量x-生产x只玩具熊猫的成本=利润,另外要求我们熟练掌握配方法求二次函数最值的应用.

练习册系列答案
相关题目
12. 如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
 如图是由几个相同的小正方体摆成的组合图形,其主视图为( )
如图是由几个相同的小正方体摆成的组合图形,其主视图为( )| A. |  | B. |  | C. |  | D. |  |
9.如果从-1,2,3三个数中任取一个数记作m,又从0,1,-2三个数中任取一个数记作n,那么点P(m,n)恰在第四象限的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |

 如图,一次函数y=kx+b与反比例函数的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数的图象交于A(1,4),B(4,n)两点. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.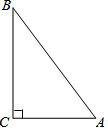 已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.
已知在△ABC中,∠ACB=90°,AB=10,cosA=$\frac{3}{5}$(如图),将△ABC绕着点C旋转,点A、B的对应点分别记为A′、B′,A′B′与边AB相交于点E.如果A′B′⊥AC,那么线段B′E的长为$\frac{24}{5}$.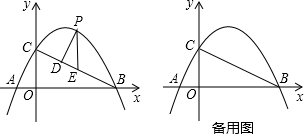
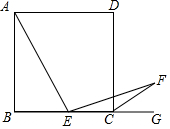 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交正方形的外角∠DCG的平分线于点F,设BE=x,△ECF的面积为y,下列图象中,能大致表示y与x的函数关系的是( )
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交正方形的外角∠DCG的平分线于点F,设BE=x,△ECF的面积为y,下列图象中,能大致表示y与x的函数关系的是( )