题目内容
11. 如图,一次函数y=kx+b与反比例函数的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数的图象交于A(1,4),B(4,n)两点.(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB的值最小.
分析 (1)把A点坐标代入反比例函数的解析式,即可求出反比例函数的解析式;
(2)求出B点坐标,把A、B的坐标代入一次函数的解析式,根据待定系数法,即可得出一次函数的解析式;
(3)求出点A的关于x轴的对称点坐标A′,然后将A′B的解析式求出,令y=0代入AC的解析式即可求出P的坐标.
解答 解:(1)设反比例函数的解析式为y=$\frac{m}{x}$(m≠0),
∵点A(1,4)在反比例函数的图象上,
∴m=1×4=4,
∴反比例函数的表达式为y=$\frac{4}{x}$;
(2)∵点B(4,n)也在反比例函数y=$\frac{4}{x}$的图象上,
∴n=$\frac{4}{4}$=1,即B(4,1),
把点A(1,4),点B(4,1)代入一次函数y=kx+b中,
得$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴一次函数的表达式为y=-x+5;
(3) ∵A′与A关于x轴对称,
∵A′与A关于x轴对称,
∴A′(1,-4),
设直线A′B的解析式为:y=ax+b,
将A′(1,-4)和B(4,1)代入y=ax+b,
∴解得$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{b=-\frac{17}{3}}\end{array}\right.$
∴一次函数的解析式为:y=$\frac{5}{3}$x-$\frac{17}{3}$,
令y=0代入y=$\frac{5}{3}$x-$\frac{17}{3}$,解得x=$\frac{17}{5}$,
∴P($\frac{17}{5}$,0).
点评 本题考查了轴对称的性质,用待定系数法求函数的图象,一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力,题目比较好,难度适中.

| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
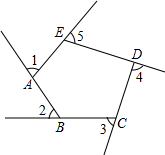 如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°.
如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°.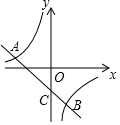 如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.
如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.